引言
从题目也可以看出本章主要介绍的是概率论的相关知识,概率论在机器学习分类和回归的相关判别中有很大的应用,本章就来看看概率论的相关知识吧!
正文
随机变量和概率分布
- 随机变量:取值任意
- 离散型:有限多取值
- 连续性:无限多取值
- 概率分布
- 离散型:概率质量函数
- 单变量
P(X=x1,...xn)=... - 联合概率分布
P(x = x; y = y)
- 连续性: 概率密度函数p要满足以下条件
- p 的定义域必须是x 所有可能状态的集合。
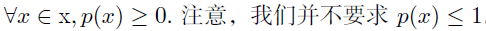
- $\int p(x)dx=1$
我们可以对概率密度函数求积分来获得点集的真实概率质量
边缘概率
我们知道了一组变量的联合概率分布,但想要了解其中一个子集的概率分布。这种定义在子集上的概率分布被称为边缘概率分布。
有变量x和y,我们知道联合概率P(x,y),可以根据以下法则求P(x):
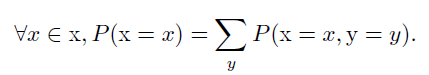
通常每行表示不同的x值,每列表示不同的y值
条件概率
在X=x的情况下,Y=y的概率可表示为:
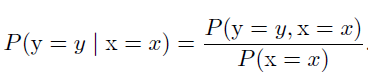
- 链式法则
任何多维随机变量的联合概率分布,都可以分解成只有一个变量的条件概率相乘的形式:
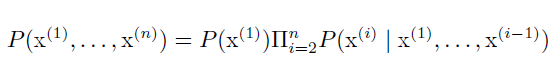
如:
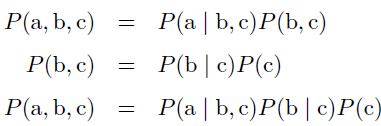
独立和条件独立
- 相互独立
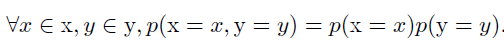
- 条件独立
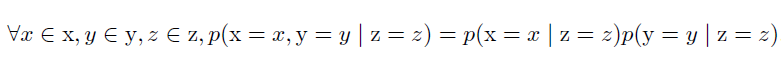
期望、方差和协方差
- 期望:线性的
- 离散型
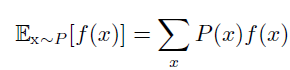
- 连续型
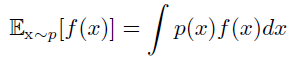
- 离散型
- 方差:平方型
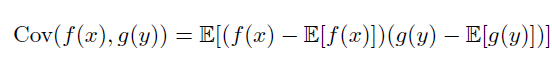
- 协方差
下面介绍一下协方差矩阵的求法:
给定一组样本向量x1,x2,...xn,每个向量都是d维的,其中:
$x_i=[x_,x_,...x_]$,
假设给定样本(1,2,3),(3,1,1),可以按照以下步骤求解协方差矩阵:
- 生成矩阵X
注意这里每行代表一个样本(要看清给定向量有没有转置符号,避免行列弄反)
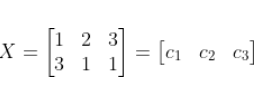
- 求每个维度均值
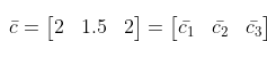
- X每一列减去均值
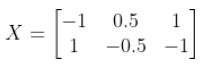
其中
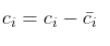
- 计算协方差矩阵
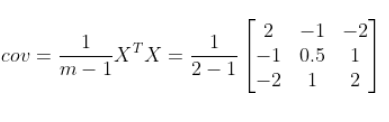
其中m为向量个数
常用概率分布
Bernouli分布
单个二值随机变量的分布。它由单个参数$\phi \in [0,1]$控制,ϕ 给出了随机变量等于1 的概率。它具有如下的一些性质:
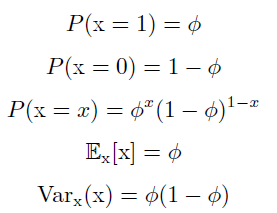
MultiBernouli分布
是指在具有k 个不同状态的单个离散型随机变量上的分布,Multinoulli 分布由向量$p\in[0,1]^$参数化,其中每一个分量$p_i$表示第i 个状态的概率
高斯分布
一维
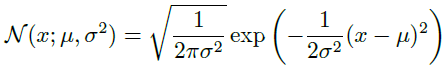
- 均值: $\mu$
- 方差: $\sigma^2$
一种更高效的参数化分布的方式是使用参数$\beta \in(0,+\infty)$,来控制分布的精度(precision)(或方差的倒数)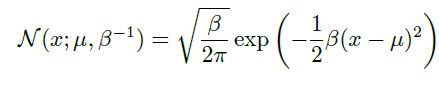
高斯分布在实际中具有很广泛运用,体现在:
- 很多建模实际情况贴近正太分布
- 由中心极限定理说明很多独立随机变量的和近似服从正态分布
多维
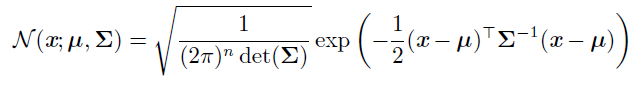
多维正态分布参数是正定对称矩阵,参数$\mu$仍然表示分布的均值,只不过现在是向量值。参数$\sum$给出了分布的协方差矩阵。我们可以使用一个精度矩阵进行替代方差:
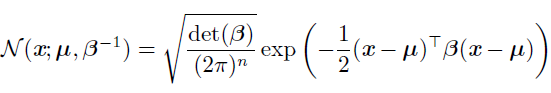
指数分布和Laplace分布
- 指数分布
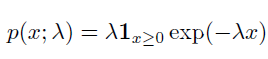
指示函数$1_{x\ge0}$来使得当x 取负值时的概率为零 - Laplace分布
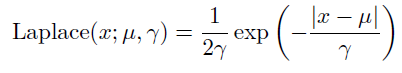
Dirac分布和经验分布
- Dirac分布:
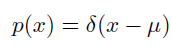
- 经验分布:
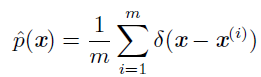
混合分布
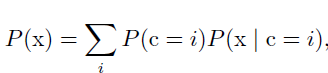
常用函数
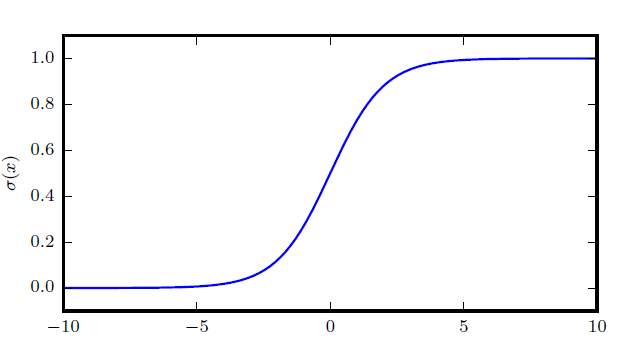
sigmoid函数
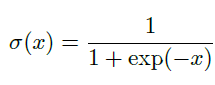
softplus函数
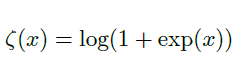
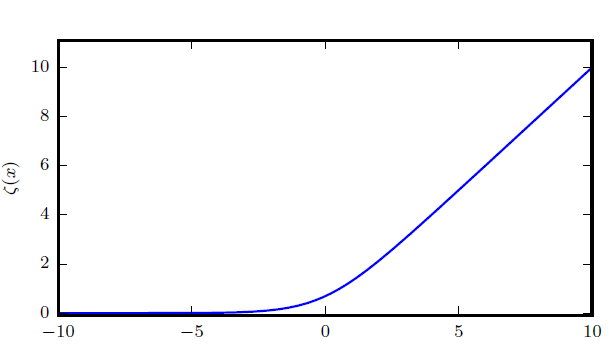
关系
这两个函数在各种运算中都存在紧密联系:
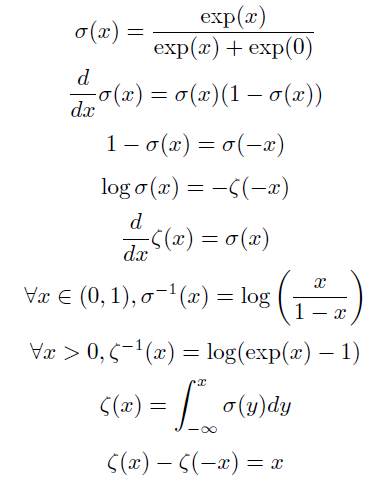
$\sigma^{-1}$也称为分对数
贝叶斯规则
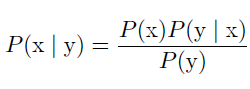
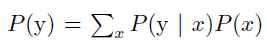
信息论
一个事件发生概率越大,包含有用信息越小,熵越小
自信息
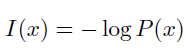
I(x) 单位是奈特(nats)。一奈特是以$\frac{1}$的概率观测到一个事件时获得的信息量,使用底数为2 的对数,单位是比特(bit)或者香农
熵
用H(x)表示:
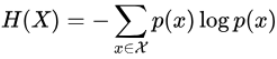
KL散度
对同一个随机变量x有两个不同分布P(x)和Q(x),可以使用KL散度来衡量分布差异:
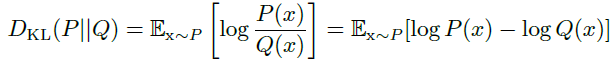
$D_=0$表示P和Q分布相同,但$D_(P|Q)\neq D_(Q|P)$
交叉熵
- 定义:把来自一个分布q的消息使用另一个分布p的最佳代码传达的平均消息长度
- 计算:
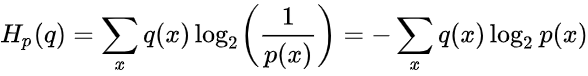
每日一语
我想拿快递!!
