西瓜书第二章-模型评估与选择

1.经验误差与过拟合

把样本中所有最后预测的正负样本分成TP、TN、FP、FN，分别表示正确分类为正样本、负样本，错误分类为正样本、负样本，有以下概念：

基本概念

• 准确率：预测正确的结果占总样本的百分比，虽然准确率能够判断总的正确率，但是在样本不均衡的情况下，并不能作为很好的指标来衡量结果
  $acc=\frac{TP+TN}{TP+TN+FP+FN}$
• 精确率：在被所有预测为正的样本中实际为正样本的概率，精确率代表对正样本结果中的预测准确程度，准确率则代表整体的预测准确程度，包括正样本和负样本
  $precise=\frac{TP+FP}$
• 召回率: 在实际为正的样本中被预测为正样本的概率
  $recall=\frac{TP+FN}$
• 经验误差与泛化误差：在训练集上的误差称为经验误差，在测试集上的误差称为泛化误差
• 欠拟合和过拟合：
  口语化理解：在训练集上表现太差（太看重训练集以至于不能适应新的数据）

数据集划分

• 留出法：训练集+测试集 训练/测试集的划分要尽可能保持数据分布的一致性，避免困数据划分过程引入额外的偏差而对最终结果产生影响，例如在分类任务中至少要保持样本的类别比例相似.如果从来样(sampling) 的角度来看待数据集的划分过程，则保留类别比例的采样方式通常称为"分层采样"。
  单次使用留出法得到的估计结果往往不够稳定可靠，在使用留出法时，一般要采用若干次随机划分、重复进行实验评估后取平均值作为留出法的评估结果

• 交叉验证法：先将数据集D划分为k个大小相似的互斥子集，$D=D_1\cup D_2 \cdots \cup D_k, D_i \cap D_j=\oslash(i \neq j)$ 每个子集Di 都
  尽可能保持数据分布的一致性，即从D 中通过分层采样得到. 然后，每次用k-1 个子集的并集作为训练集，余下的那个子集作为测试集;这样就可获得k组训练/测试集，从而可进行k次训练和测试，最终返回的是这k个测试结果的均值，交叉验证法评估结果的稳定性和保真性在很大程度上取决于k的取值，为强调这一点，通常把交叉验证法称为" k 折交叉验证"，k通常=10
  与留出法相似，将数据集D 划分为k 个子集同样存在多种划分方式.为减小因样本划分不同而引入的差别， k 折交叉验证通常要随机使用不同的划分重复p 次，最终的评估结果是这p 次k折交叉验证结果的均值
  假定数据集 D 中包含m个样本，若令 k=m ， 则得到了交叉验证法的一个特例:留一法，留一法虽然准确率较高，但是数据集较大时计算成本太高

• 自助法：给定包含m 个样本的数据集D，我们对它进行采样产生数据集D': 每次随机从D 中挑选一个样本将其拷贝放入D' 然后再将该样本放回初始数据集D 中，使得该样本在下次采样时仍有可能被采到，这个过程重复执行m 次后我们就得到了包含m个样本的数据集D'，这就是自助采样的结果.显然， D 中有一部分样本会在D'中多次出现，而另一部分样本不出现.可以做一个简单的估计，样本在m 次采样中始终不被采到的概率是$(1-\frac{1})^$ ，由微积分极限可知：
  
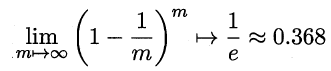
  即通过自助采样，初始数据集D中约有36.8% 的样本未出现在采样数据集D'中.于是我们可将D' 用作训练集， D\D' 用作测试集。
  自助法在数据集较小、难以有效划分训练/测试集时很有用

• 调参与最终模型：不可能尝试每一个参数值，现实中常用的做法是对每个参数选定一个范围和变化步长，例如在[0，0.2] 范围内以0.05 为步长，则实际要评估的候选参数值有5 个，最终是从这5个候选值中产生选定值，在训练的过程中我们通常把训练集拿出一部分用于改进参数。

2. 性能度量

在预测任务中，给定样例集D = {(X1, Y1) , (X2, y2)， . . . , (Xm, Ym)} ，其中yi是示例Xi 的真实标记.要评估学习器f 的性能，就要把学习器预测结果f(x)与真实标记y进行比较，通常采用均方误差。

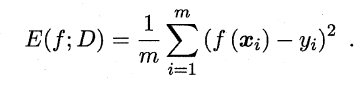
用概率密度函数：

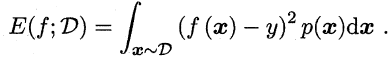
常见指标

• 查准率与查全率：就是前面介绍的precise和recall
  查准率和查全率是一对矛盾的度量.一般来说，查准率高时，查全率往往
  偏低;而查全率高时，查准率往往偏低，根据对哪种需求更高选择对应指标。
• P-R曲线：在很多情形下我们可根据学习器的预测结果对样例进行排序，排在前面的是学习器认为"最可能"是正例的样本，排在最后的则是学习器认为"最不能"是正例的样本.按此顺序逐个把样本作为正例进行预测，则每次可以计算出当前的查全率、查准率以查准率为纵轴，查全率为横轴作图，就得到了查准率-查全率曲线，简称" P-R 曲线"，如下图所示：
  
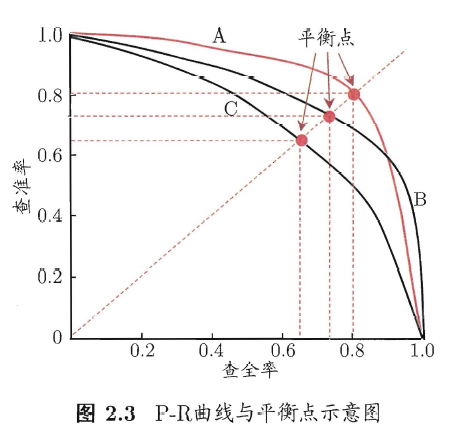
  P-R 图直观地显示出学习器在样本总体上的查全率、查准率.在进行比较时，若一个学习器的P-R 曲线被另一个学习器的曲线完全"包住" ， 则可断言后者的性能优于前者， 例如上图中学习器A 的性能优于学习器C; 如果两个学习器的P-R 曲线发生了交叉，例如上图中的A 与B ，则难以一般性地断言两者孰优孰劣，这时通过比较P-R曲线下面积大小来表征，由于面积计算比较麻烦，可以通过比较平衡点（查准率和查全率相等时的取值）
• F1 score：最常用度量指标
  
  根据对查准率和查全率的偏好不同修正为：
  
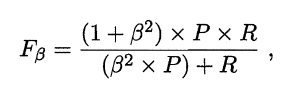
  其中β度量了查全率对查准率的相对重要性，β=1时退化为标准的F1; ß> 1 时查全率有更大影响; ß < 1 时查准率有更大影响.
  很多时候我们寄多个二分类混淆矩阵，例如进行多次训练/测试，每次得到一个混淆矩阵;或是在多个数据集上进行训练/测试，希望估计算法的"全局"性能;甚或是执行多分类任务，每两两类别的组合都对应一个混淆矩阵，总之，我们希望在n 个二分类混淆矩阵上综合考察查准率和查全率，一种直接的做法是先在各混淆矩阵上分别计算出查准率和查全率，记为$(P_1,R_1),(P_2,R_2),\cdots (P_n,R_n)$ ， 再计算平均值，这样就得到"宏查准率" (micro-P) 、"宏查全率" (micro-R) ，以及相应的"宏F1" (micro-F1):
  
  

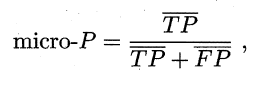
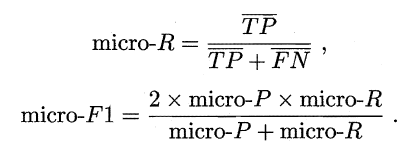
ROC

很多学习器是为测试样本产生一个实值或概率预测，然后将这个预测值与一个分类阈值(threshold)进行比较，若大于阈值则分为正类，否则为反类，我们可将测试样本进行排序，"最可能"是正例的排在最前面，"最不可能"是正例的排在最后面.这样，分类过程就相当于在这个排序中以某个"截断点" (cut point)将样本分为两部分，前一部分判作正例，后一部分则判作反例。
在不同的应用任务中，我们可根据任务需求来采用不同的截断点，例如若我们更重视"查准率"，则可选择排序中靠前的位置进行截断;若更重视"查全率"，则可选择靠后的位置进行截断，需要考虑排序位置。
ROC 全称是"受试者工作特征" (Receiver Operating Characteristic) 曲线，我们根据学习器的预测结果对样例进行排序，按此顺序逐个把样本作为正例进行预测，每次计算出两个重要量的值，分别以它们为横、纵坐标作图'就得了"ROC 曲线与P-R 曲线使用查准率、查全率为纵、横轴不同， ROC 曲线的纵轴是"真正例率" (True Positive Rate，简称TPR) ，横轴是"假正例率" (False PositiveRate，简称FPR) ，基于表2.1 中的符号，两者分别定义为：

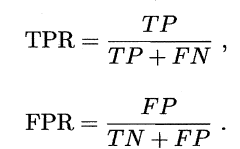
下图所示为ROC曲线和AUC曲线：

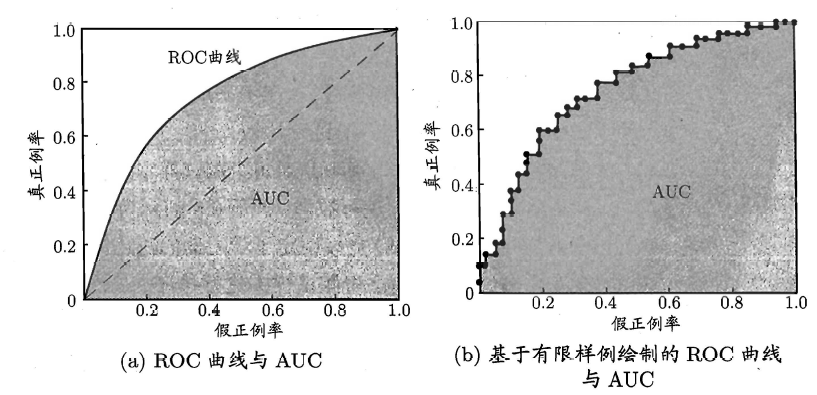
• 如何拟合ROC
  给定m+个正例和m-个反例，根据学习器预测结果对样例进行排序，然后把分类阔值设为最大，即把所有样例均预测为反例，此时真正例率和假正例率均为0 ， 在坐标(0,0) 处标记一个点然后，将分类阐值依次设为每个样例的预测值，即依次将每个样例划分为正例.设前一个标记点坐标为(x,y) ， 当前若为真正例，则对应标记点的坐标为$(x,y+\frac{1}{m^{+})$，当前是假正例，对应点坐标为$(x+\frac{1}{m}-},y)$，然后顺序连接即可。

AUC

AUC 可通过对ROC 曲线下各部分的面积求和而得. 假定ROC 曲线是由坐标为{(x1,y1),...(xm,ym)},AUC可近似为：

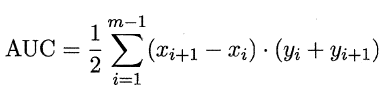
形式化地看， AUC 考虑的是样本预测的排序质量，因此它与排序误差有紧密联系，给定m+个正例和m-个反例，令D+ 和D-分别表示正、反例集合，则排序"损失" (loss) 定义为:

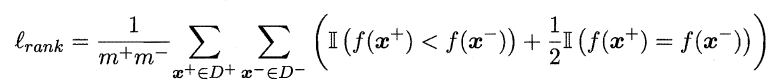
从公式可以看出，若正例预测值小于反例，则记为1个"罚分"，若相等记为0.5个，$l_$是ROC曲线之上的面积，从而：
$AUC=1-l_$

代价敏感错误率和代价曲线

在现实生活中，不同类别的判别错误重要程度不一样（癌症就是个例子），假设判别的由i个类别，共有j中判别方案，则可以得到代价矩阵$Cost_$，表示把第i个类别误判为j的代价，二分类如下图所示：

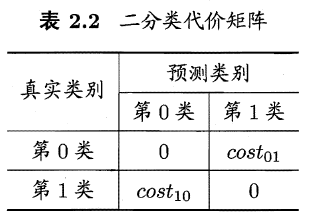
若Cost(01)≠Cost(10)，ROC 曲线不能直接反映出学习器的期望总体代价，而
"代价曲线" (cost curve) 则可达到该目的.代价曲线图的横轴是取值为[0，1]的正例概率代价：

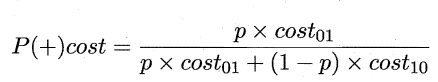
其中p 是样例为正例的概率;纵轴是取值为[0 ，1] 的归一化代价：
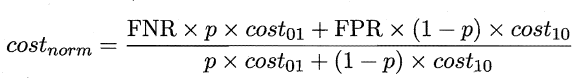其中FPR是假正例率， FNR=1 - TPR 是假反例率。

• 代价曲线绘制方法
  ROC 由线上每点对应了代价平面上的一条线段，设ROC 曲线上点的坐标为(TPR， FPR) ，则可相应计算出FNR，然后在代价平面上绘制一条从(0，FPR) 到(l， FNR) 的线段，线段下的面积即表示了该条件下的期望总体代价;如此将ROC 曲线土的每个点转化为代价平面上的一条线段，然后取所有线段的下界，围成的面积即为在所有条件下学习器的期望总体代价，如下图所示：
  

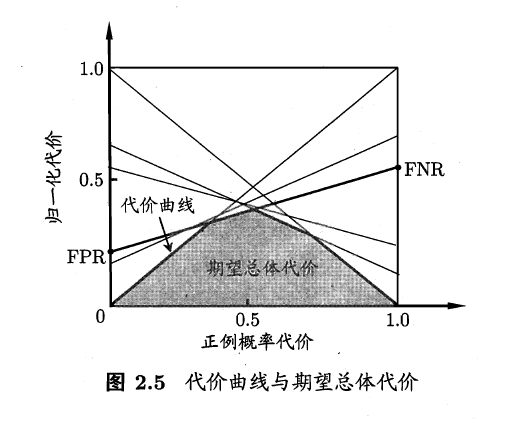
3.假设检验

t检验

训练错误和测试错误不一定一样，可根据测试错误率估推出泛化错误率的
分布.泛化错误率为ε的学习器在一个样本上犯错的概率是ε; 测试错误率$\hat \epsilon$意味
着在m 个测试样本中恰有$m\times \hat \epsilon$个被误分类.假定测试样本是从样本总体分布
中独立采样而得，那么泛化错误率为ε 的学习器将其中m' 个样本误分类、其
余样本全部分类正确的概率是$\epsilon^{{m'}(1-\epsilon)}{m-m'}$,由此可估算出其恰将Ê x m 个样本误分类的概率如下式所示，也表达了在包含m 个样本的测试集上,泛化错误率为ε的学习器被测得测试错误率为$\hat \epsilon$的概率:

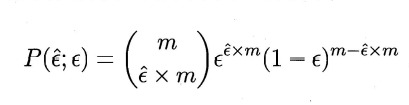
使用t检验法，考虑假设$\epsilon \lt \epsilon_0$，则在$1-\alpha$的概率内所能观测到的最大错误率如下式计算:

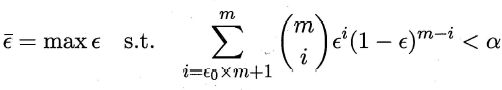
此时若测试错误率$\hat \epsilon$小于临界值$\bar \epsilon$，则根据二项检验可得出结论:在α 的显著度下，假设$\epsilon \lt \epsilon_0$不能被拒绝，即能以1-α的置信度认为，学习器的泛化错误率不大于$\epsilon_0$; 否则该假设可被拒绝，即在α 的显著度下可认为学习器的泛化错误率大于$\epsilon_0$，一般可进行k次t检验，求均值和方差：

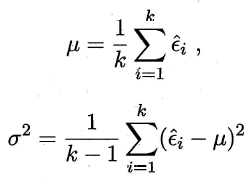
考虑到这k 个测试错误率可看作泛化错误率$\epsilon_0$的独立采样，则变量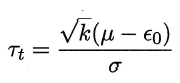服从自由度为k-l 的t 分布（概率论知识）

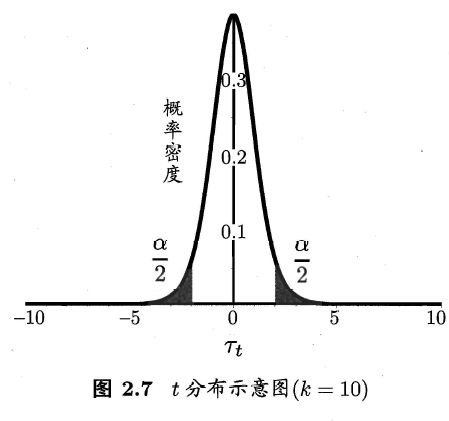
考虑双边α/2临界值，通常查表。

交叉验证t检验

对两个学习器A 和B ，若我们使用k 折交叉验证法得到的测试错误率分别为:

其中$\epsilon_i^{A$ 和$\epsilon_i}B$是在相同的第i折训练/测试集上得到的结果，则可用k 折交叉验证"成对t 检验" (paired t-tests )来进行比较检验.这里的基本思想是若两个学习器的性能相同，则它们使用相同的训练/测试集得到的测试错误率应相同，即$\epsilon_i^{A$=$\epsilon_i}B$，具体来说，对k折交叉验证产生的k 对测试错误率:

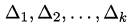
对这k个值进行t检验，计算出差值的均值μ 和方差$\sigma^2$ ，在显著度α 下，若变量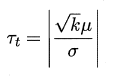
小于临界值$t_{\frac{\alpha}{2}, k-1}$则假设不能被拒绝，即认为两个学习器的性能没有显著差异， 否则可认为两个学习器的性能有显著差别，且平均错误率较小的那个学习器性能较优。实际情况k次训练样本会有重叠，可采用"5 x 2 交叉验证"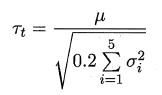，，服从自由度为5 的t 分布，其双边检验的临界值 $t_{\frac{\alpha}{2},5}$ 当α 为0.05时为2.5706 ，α= 0.1 时为2.0150

下面这些检验方法都不常见，简要介绍思想

McNemar检验

使用留出法得到两个学习器A和B分类结果差异，即两者都正确、都错误、一个正确另一个错误的样本数，如下表所示：

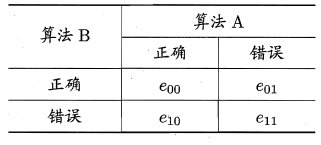
若我们做的假设是两学习器性能相同，则应有e01 = e10，那么变量
|e01-e10| 应当服从正态分布，且均值为1 ，方差为e01+e10.变量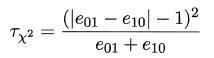，服从自由度为1 的χ2 分布，给定显著度α，当以上变量恒小于临界值$\chi^2$时，不能拒绝假设，即认为两学习器的性能没有显著差别，否则拒绝假设，即认为两者性能有显著差别，且平均错误率较小的那个学习器性能较优。

Friedman 检验与Nemenyi后续检验

前面介绍的都是在一个数据集上比较多种算法，那么在不同数据集上如何比较呢？
假定我们用Dl、D2 、D3 和D4 四个数据集对算法A 、B 、C 进行比较.首先，使用留出法或交叉验证法得到每个算法在每个数据集上的测试结果，然后在每个数据集上根据测试性能由好到坏排序，1，2，...，若算法测试效果相同则平分均值，否则使用Friedman检验来比较

• Friedman检验
  我们在N个数据集上比较k个算法，令$r_i$表示第i个算法的平均序值，为简化讨论，暂不考虑平分序值的情况，则$r_i$服从正态分布，其均值和方差分别为(k+ 1)/2 和$(k^2-1)/12$，变量
  
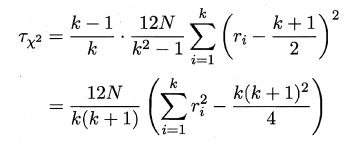
  在k 和N 都较大时，服从自由度为k-1 的χ2 分布，通常选用以下变量进行判断
  
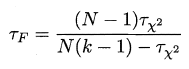
  $\tau_F$服从k-1和（K-1）（N-1）的F分布，下表给出了常用临界值
  
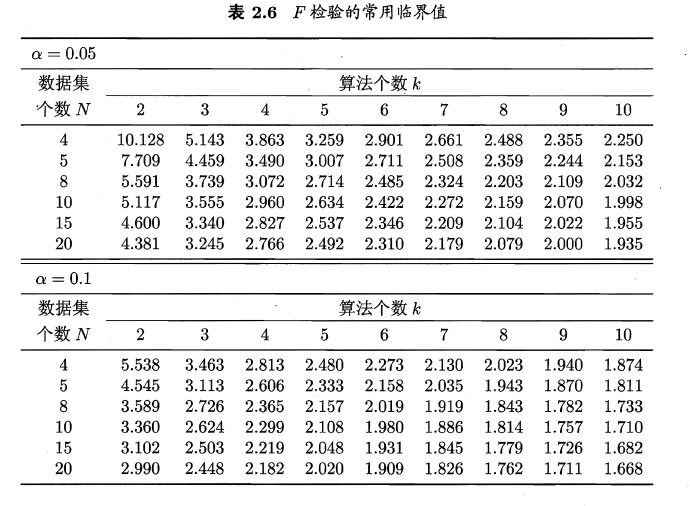
• Nemenyi检验
  检验计算出平均序值差别的临界值域
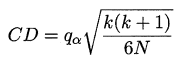  ，下面给出了α=0.01和0.1时常见判别值，若两个算法的平均序值超过了临界值域CD，以相应的置信度拒绝"两个算法性能相同"这一假设。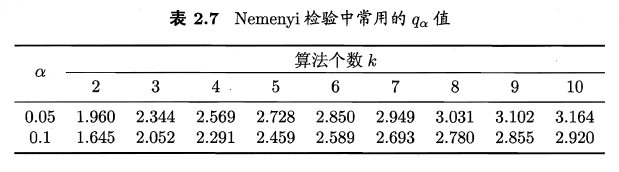
  上述检验比较可以直观地用Friedman 检验图显示横轴是平均序值.对每个算法，用一个圆点显示其平均序值，以圆点为中心的横线段表示临界值域的大小.然后就可从图中观察，若两个算法的横线段有交叠，则说明这两个算法没有显著差别，否则即说明有显著差别.
  
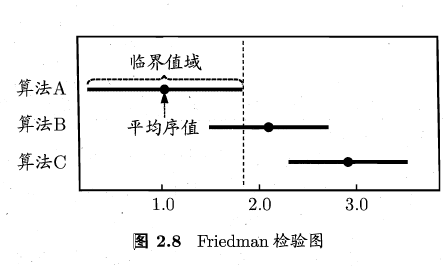
  如上图A和B没有显著差异，A和C有显著差异。

偏差和方差

偏差和方差关系可以通过以下公式推导：


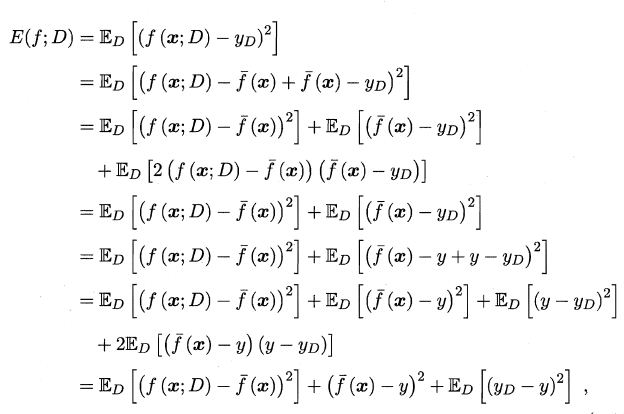
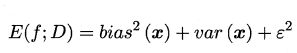
泛化误差可分解为偏差、方差与噪声之和.

• 偏差：度量了学习算法的期望预测与真实结果的偏离程度，即刻画了学习算法本身的拟合能力
• 方差：度量了同样大小的训练集的变动所导致的学习性能的变化，即刻画了数据扰动所造成的影响
• 噪声：表达了在当前任务上任何学习算法所能达到的期望泛化误差的下界，即刻画了学习问题本身的难度
  泛化性能是由学习算法的能力、数据的充分性以及学习任务本身的难度所共同决定的.给定学习任务，为了取得好的泛化性能，则需使偏差较小，即能够充分拟合数据，并且使方差较小，即使得数据扰动产生的影响小.