Dynamic Snake Convolution based on Topological Geometric Constraints for Tubular Structure Segmentation

摘要

拓扑管状结构(如血管和道路)的准确分割在各个领域都至关重要，可以确保下游任务的准确性和效率。然而，许多因素使任务复杂化，包括薄的局部结构和可变的全局形态。在这项工作中，我们注意到管状结构的特殊性，并利用这一知识指导我们的DSCNet在三个阶段同时增强感知:特征提取、特征融合和损失约束。首先，我们提出了一种动态蛇形卷积，通过自适应聚焦细长和弯曲的局部结构来准确捕捉管状结构的特征。随后，我们提出了一种多视角特征融合策略，以补充特征融合过程中对多个视角特征的关注，确保保留来自不同全局形态的重要信息。最后，提出了一种基于持久同调的连续性约束损失函数，以更好地约束分割的拓扑连续性。在二维和三维数据集上的实验表明，与几种方法相比，我们的DSCNet在管状结构分割任务上具有更好的准确性和连续性。我们的代码是公开的。

1. 介绍

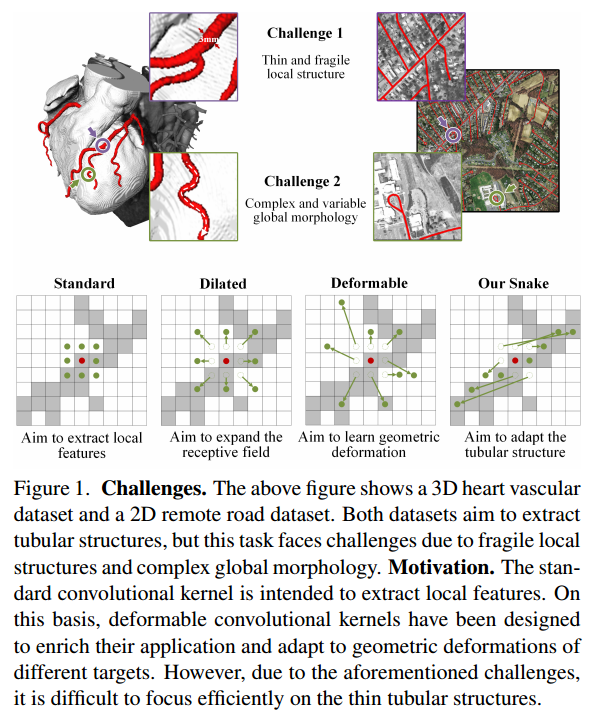
拓扑管状结构的准确分割是保证下游任务精度和效率的关键。在临床应用中，血管的清晰描绘是计算血流动力学的关键先决条件，它存在于放射科医师病灶定位与诊断。在遥感应用中，完整的道路分割为路线规划提供了坚实的基础。无论在哪个领域，这些结构都具有薄而曲折的共同特征，这使得它们由于在图像中所占的比例很小而难以捕捉。因此，迫切需要增强对薄管结构的感知。然而，由于以下困难，仍然具有挑战性:(1)局部结构薄而脆弱，如图1所示，薄结构仅占整体图像的一小部分，像素组成有限。此外，这些结构容易受到复杂背景的干扰，使得模型难以精确识别目标的细微变化。因此，模型可能难以区分这些结构，从而导致分割的断裂。
(2)复杂多变的全局形态。图1显示了薄管状结构的复杂多变的形态，即使在同一图像中也是如此。在不同区域的目标中观察到形态变化，这取决于分支的数量、分支的位置和路径长度。当数据呈现出前所未有的形态结构时，模型可能会倾向于过度拟合已经看到的特征，从而导致弱泛化。

近年来，许多研究提出引入领域知识(如几何拓扑和树形结构)来指导模型更好地感知管状结构的特征，从而提高局部分割的准确性，保持全局形态的连续性。现有方法大致可分为三类:(1)基于网络的方法[7、12、31、28、14、8]根据管状结构的特性设计特定的网络架构，引导模型关注关键特征。然而，由于管状结构的比例较小，网络不可避免地会失去对相应结构的感知。(2)基于特征的方法[21,33,15,35,20]通过为模型补充额外的特征表示来增强对管状结构特定几何和拓扑特征的理解。然而，一些冗余的特征表示加剧了计算负担，同时对模型没有提供积极的影响。(3)基于损失的方法[24,29,1,30]在训练过程中采用测量方法来补充约束，通常通过损失函数。这些方法加强了对分割的严格约束。在此基础上，结构损失与拓扑角度的连续性约束相结合，将有可能进一步提高管柱分割的准确性。

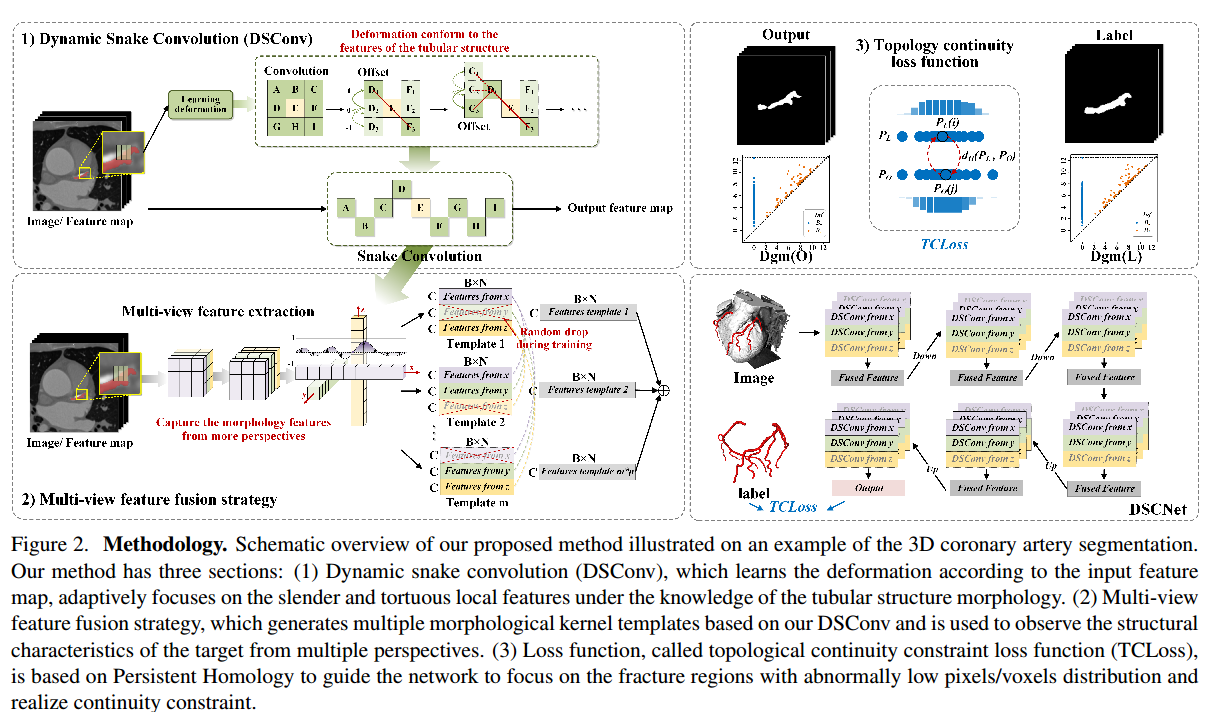
为了解决上述问题，我们提出了一种新的框架DSCNet，该框架包括管状感知卷积核、多视图特征融合策略和拓扑连续性约束损失函数。(1)针对局部结构薄而脆弱的比例小，难以被模型关注的问题，我们提出了动态蛇形卷积(DSConv)，通过自适应关注管状结构的薄而弯曲的局部特征来增强几何结构的感知。与[6]不同，[6]使网络完全自由地学习几何变化，从而导致感知区域漫游，特别是在薄管结构上，我们的DSConv考虑了管状结构的蛇形形态，并通过约束来补充自由学习过程，从而允许有针对性地增强管状结构的感知。(2)针对复杂多变的全局形态挑战，提出了一种多视角特征融合策略。在该方法中，我们基于DSConv生成多个形态学核模板，从多个角度观察目标的结构特征，并通过总结典型的重要特征来实现高效的特征融合。(3)针对管状结构分段容易发生断裂的问题，提出了一种基于持续同源性(PH)的拓扑连续性约束损失函数(TCLoss)。PH[9,19,5]响应拓扑特征从出现到消失的过程。它从高维噪声数据中获得充分的拓扑信息。相关的贝蒂数是描述拓扑空间连通性的一种方式。与[30,10]不同的是，我们的TCLoss将PH值与点集相似度结合起来，引导网络专注于具有异常像素/体素分布的裂缝区域，从拓扑角度实现连续性约束。

总之，我们的工作提出了一种新的知识融合框架，解决了薄管结构的困难，具体贡献有三个方面。(1)提出了一种动态蛇形卷积算法，自适应聚焦于细长和弯曲的局部特征，在二维和三维数据集上实现管状结构的精确分割。我们的模型使用内部和外部测试数据进行了彻底验证。(2)提出多视角特征融合策略，补充对多视角重要特征的关注。(3)提出一种基于持久同调的拓扑连续性约束损失函数，较好地约束了分割的连续性。

2. 相关工作

2.1 基于网络设计的方法

人们提出了各种方法，通过根据管状结构的形态设计特定的网络结构和模块来获得更好的性能。(1)提出了以著名的展开卷积[32]和变形卷积[6]为代表的基于卷积核设计的方法来处理cnn固有的有限几何变换，在复杂的检测和分割任务上表现出优异的性能。这些方法[7,34,12,31]也是为了动态感知物体的几何特征，以适应形态多变的结构。例如，[12]中提出的DUNet将可变形卷积整合成u形结构并根据血管的大小和形状自适应地调整接受野。(2)提出了基于网络体系结构设计的方法来学习管状结构的特殊几何拓扑特征。提出了用点集表示管状结构的PointScatter[28]，作为管状结构提取任务的分割模型的替代方案。[14]提出了一个树状结构的卷积门控循环单元来明确地模拟冠状动脉的拓扑结构。不同于上述允许模型完全自由学习几何变化的思路，考虑到过度随机性带来的收敛难度的局限性，以及模型可能会关注目标的意外区域。我们的工作整合了管状结构形态学的领域知识，在特征提取过程中稳定地增强了对管状结构的感知。

2.2 基于特征融合的方法

基于特征融合的方法[35,15,33,21,20]通过向模型中补充额外的特征信息来增强管状结构的表征。考虑到管状结构的拓扑结构和稀疏性，[35]提出了一种在两个网络之间进行跨网络多尺度特征融合的方法，以有效支持高质量的血管分割。在[15]中，研究了一种基于深浅层次特征融合的全局transformer和双局部关注网络，以同时捕获全局和局部特征。[33]提出融合上下文解剖信息和血管拓扑结构，实现精确的管状结构分割。在我们的工作中，我们提出了一种多视角特征融合策略，以补充对多视角重要特征的关注。在该策略中，我们基于DSConv生成大量形态学核模板，从多个角度观察目标的结构特征，并通过总结基本标准特征来实现特征融合，从而提高模型的性能。

2.3 基于损失函数的方法

基于损失函数的方法[24,29,1]引入测量方法来补充训练过程中的约束。这些方法加强了对管状结构分割的强约束。[24]引入了一种称为中心线骰子的相似性度量，它是在分割蒙版和骨架的交点上计算的。[29]提出了一种几何感知的管状结构分割方法——深度距离变换(Deep Distance Transform, DDT)，该方法结合了经典的骨架化距离变换和管状结构分割的直觉。这些方法注重管状结构分割的连续性，但骨架的不精确和偏移会影响约束的精度。[1]提出了一种捕获预测分割拓扑一致性的相似度指标，并设计了一种基于形态闭合算子的损失函数用于管状结构分割。在[30]中，拓扑数据分析方法与几何深度学习模型相结合，用于3D对象的细粒度分割。这些方法将捕获拓扑对象的特征。受此启发，我们的工作提出了一种拓扑连续性约束损失函数(TCLoss)，从拓扑角度更好地约束了分割的连续性。我们的TCLoss在训练过程中逐渐引入基于Persistence Homology[27,2]的约束，引导网络聚焦于断裂区域，实现连续性。

3. 方法

我们的方法旨在同时处理薄管结构的二维和三维特征图。为了简单起见，我们的模块都是用2D描述的，我们的开源中也提供了对3D的详细扩展。

3.1 动态蛇形卷积

在本节中，我们讨论如何执行动态蛇形卷积(DSConv)来提取管状结构的局部特征。标准二维卷积坐标为K，中心坐标为Ki = (xi, yi)。膨胀系数为1的3 × 3核K表示为: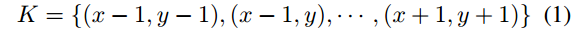

为了使卷积核更灵活地关注目标的复杂几何特征，受[6]的启发，我们引入了变形偏移量∆。然而，如果让模型自由学习变形偏移量，则感知场容易偏离目标，特别是在薄管结构的情况下。因此，我们采用迭代策略(图3)，对每个待处理的目标依次选择以下观察位置，这样既保证了注意力的连续性，又不会因为变形偏移量大而使感觉范围过于分散。

在DSConv中，我们在x轴和y轴方向上拉直标准卷积核。我们考虑一个大小为9的卷积核，以坐标轴方向为例，K中每个网格的具体位置表示为:Ki±c = (xi±c, yi±c)，其中c ={0,1,2,3,4}表示与中心网格的水平距离。卷积核K中每个网格位置Ki±c的选择是一个累积过程。从中心位置Ki开始，距离中心网格的位置取决于前一个网格的位置:Ki+1与Ki相比增加了一个偏移量∆= {δ|δ∈[- 1,1]}，因此，偏移量需要为Σ，从而确保卷积核符合线性形态结构。图3在x轴方向上为:

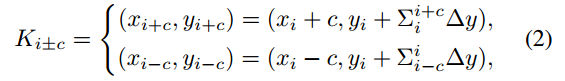
式2在y轴方向上为:

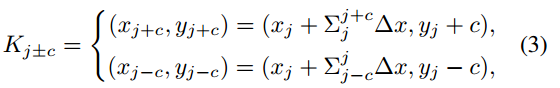
由于偏移量∆通常为分数，双线性插值实现如下:

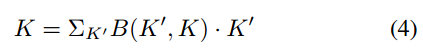
式中，K为式2、式3的分数阶位置，K′枚举所有积分空间位置，B为双线性插值核，分为两个一维核，分别为:

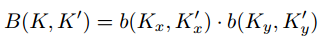
如图3所示，由于二维(x轴，y轴)的变化，我们的DSConv在变形过程中覆盖了9 × 9的范围。DSConv在动力结构的基础上更好地适应细长管状结构，从而更好地感知关键特征。

3.2 多视角特征融合策略

本节讨论实现多视图特征融合策略，以指导模型从多个角度补充对基本特征的关注。对于每一个K，分别从x轴和y轴上提取第1层的两个特征映射fl(Kx)和fl (Ky)，表示为:

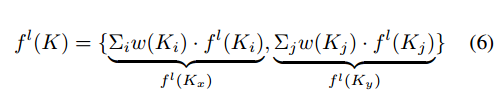
其中w(Ki)表示Ki位置的权重，第l层卷积核K提取的特征采用累积法计算。根据式6，我们提取m组特征为t1，其中包含DSConv的不同形态:

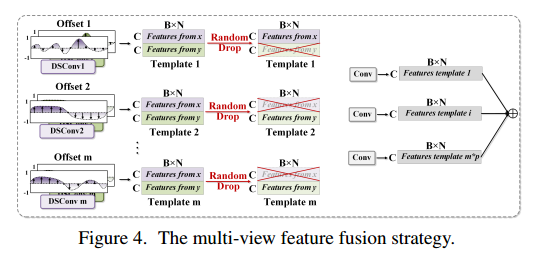
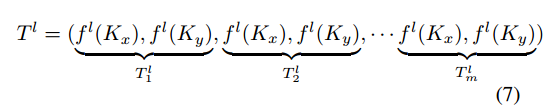
多模板特征融合不可避免地会带来冗余噪声。因此，在训练阶段引入随机丢弃策略rl(图4)，在不增加额外计算负担的情况下提高模型性能，防止过拟合，则式7为:

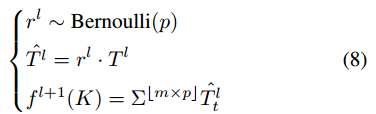
其中p是随机下降的概率，r l满足伯努利分布。在训练阶段保存最优丢弃策略，并在测试阶段指导模型融合关键特征。

3.3 拓扑连续性约束损失

在本节中，我们讨论了如何实现基于持久同调的拓扑连续性约束损失(TCLoss)来约束分割的连续性。复杂结构中的几何和拓扑信息是帮助模型理解连续结构的关键线索。利用拓扑数据分析工具提取隐藏在复杂管状结构中的基本特征。

我们的目标是构建数据的拓扑结构，并提取复杂管状结构中的高维关系，表示为持久性条形码和持久性同源性(persistence Homology, PH)，如图5所示。

给定G的n维拓扑结构，同调类[9,19]是一个由n个流形组成的等价类，这些流形在G内可以相互变形，其中0维和1维是连通的分量和柄。采用PH计算拓扑特征的演化，保持拓扑特征出现时间b与消失时间d之间的周期[30]。那些时期可以用一个简洁的持久性图(PD)形式来概括。它由一组点(b, d)组成。每个点(b, d)表示在b处出现并在d处消失的第d个同调类。令PD=dgm(·)表示由groundtruth L和输出O得到的持久同调。我们认为复杂管状结构中的拓扑信息在0维和1维的同源特征中是明显的，而拓扑信息包含了确定裂缝存在的关键线索。现有方法[30,5,10]使用修正的Wasserstein距离计算输出生成的点与groundtruth生成的点之间的最佳匹配，没有最优配对的离群点与对角线匹配，不参与损失计算。然而，在我们的任务中，异常点表示异常出现或消失的时间，并暗示起重要作用的错误拓扑关系。因此，我们使用Hausdorff距离来度量两组点之间的相似性：

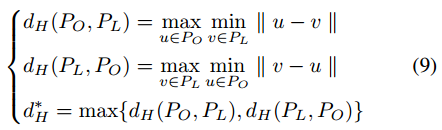
其中PO∈Dgm(O)， PL∈Dgm(L)， d * H表示双向Hausdorff距离，以n-dim点计算。我们使用的豪斯多夫距离对异常值很敏感。如式9所示，如果两组点相似，除了PO中有一个点远离PH中的任何一点外，其余点都完美叠加，则Hausdorff距离由该点决定，且较大。

然后对所有维度(n = 0,1,2，···，N)进行求和，得到LPH，并将整个TCLoss与交叉熵损失LCE作为最终损失函数lcs = LCE + $\sum_^d_{*}$进行积分。

最后，在两种损失函数的共同作用下，拓扑和精度受到约束，从而实现连续的管状分割。

4.实验设置

4.1 数据集

我们使用三个数据集，其中包含两个公共数据集和一个内部数据集来验证我们的框架。在2D中，我们评估了DRIVE视网膜数据集[25]和马萨诸塞州道路数据集[17]。在3D中，我们使用了一个叫做心脏CCTA数据的数据集。有关实验装置的细节可在补充材料中找到。

4.2 评估策略

我们进行了比较实验和消融研究，以证明我们提出的框架的优势。将经典的血管分割网络U-Net[4]与2021年提出的CS2 -Net[18]进行对比，验证其准确性。为了验证网络设计的性能，我们比较了2022年提出的用于视网膜血管分割的DCU-net[31]。为了验证特征融合的优势，我们比较了2021年提出的用于医学图像分割的Transunet[3]。为了验证损失函数约束，我们比较了2021年提出的clDice[24]和基于wasserstein -distance的TCLoss $L_$[30]。这些模型在具有精确实现的相同数据集上进行训练，并通过以下指标进行评估。计算每张图像的所有指标并取平均值。

体积分数:平均骰子系数(Dice)，相对骰子系数(RDice)[22]，中心线系数(clDice)[24]，精度(ACC)和AUC用于评估结果的性能。
拓扑误差:我们遵循[24,28]，计算基于拓扑的分数，包括Betti数β0和β1的Betti误差。同时，为了客观地验证冠状动脉分割的连续性，利用首误差(of)[23]的重叠来评价提取中心线的完整性。
距离误差:Hausdorff Distance (HD)[26]也被广泛用于描述两组点之间的相似性，被推荐用于评价薄管结构

5. 结果和讨论

在本段中，我们将以三种方式评估和分析我们提出的框架的有效性:(1)通过以下指标对我们提出的薄管结构分割任务方法的性能进行比较和验证。同时展示了不同方法的视觉效果。(2)分析了DSConv引导模型聚焦于管状结构的有效性，以及TCLoss约束分割拓扑的有效性。(3)以DRIVE数据集为例，提供了包括消融实验在内的综合实验。此外，由于篇幅限制，我们重点介绍了在其他数据集上进行的一些最重要的比较实验。结果表明，该方法在二维和三维领域都具有较强的性能。

5.1 定量评估

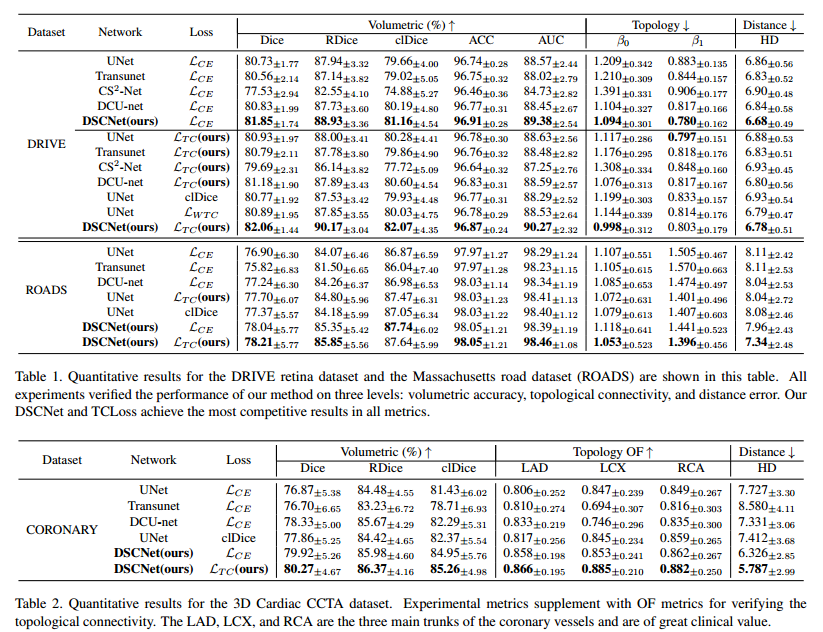
表1展示了我们的方法在每个指标上的优势，结果表明，我们提出的DSCNet在2D和3D数据集上都取得了更好的结果。

对DRIVE的评价。在DRIVE数据集上，我们的DSCNet在分割精度和拓扑连续性方面优于其他模型。在表1中，从体积精度的角度来看，我们提出的DSCNet与其他方法相比，分割效果最好，Dice为82.06%，RDice为90.17%，clDice为82.07%，ACC为96.87%，AUC为90.27%。同时，从拓扑学角度来看，我们的DSCNet与其他方法相比具有最佳的拓扑连续性，其β0误差为0.998，β1误差为0.803。结果表明，该方法更好地捕捉了细管结构的具体特征，具有更准确的分割性能和更连续的拓扑结构。如表1的第6 ~ 12行所示，在我们的TCLoss的加入下，不同的模型在分割的拓扑连续性上都有所提高。结果表明，我们的TCLoss精确地约束了模型，使其专注于失去拓扑连续性的薄管结构

道路评价。在马萨诸塞州道路数据集上，我们的DSCNet也取得了最好的结果。如表1所示，我们提出的DSCNet与TCLoss的分割效果最好，其中Dice的分割率为78.21%，RDice的分割率为85.85%，clDice的分割率为87.64%。与经典分割网络UNet的结果相比，我们的方法最多实现了1.31%的Dice, 1.78%的RDice和0.77%的clDice改进。结果表明，与其他模型相比，我们的模型在结构复杂和形态可变的道路数据集上也表现良好。

冠状动脉评价。在心脏CCTA数据集上，我们验证了我们的DSCNet在3D分割细管结构方面仍然取得了相同的最佳结果。如表2所示，与其他方法相比，我们提出的DSCNet的分割效果最好，Dice的分割率为80.27%，RDice的分割率为86.37%，clDice的分割率为85.26%。与经典分割网络UNet的结果相比，我们的方法最多实现了3.40% Dice、1.89% RDice和3.83% clDice的改进。同时，我们使用OF指标来评估分割的连续性。使用我们的方法，LAD的OF指标提高了6.00%，LCX提高了3.78%，并且对于RCA提高了3.3%(LAD、LCX和RCA是冠状动脉的重要主干)。血管连续性的改善在临床上起着至关重要的作用.

消融实验分析
以DRIVE数据集为例，消融实验证明了我们的DSCNet和TCLoss的重要性。(1)证明我们的DSCNet的有效性。表1前五行的结果表明，我们的方法更适合于细管状结构的分割。结果表明，我们提出的DSConv在模型中起着至关重要的作用，帮助网络更好地捕捉薄管结构的关键特征。(2)证明tclos的有效性。如表1的第6至第9行所示，在我们的TCLoss的加入下，不同的模型在分割的拓扑连续性方面都有所改善。结果表明，我们的TCLoss精确地约束了模型，使其专注于失去拓扑连续性的薄管结构。

5.2 定量评估

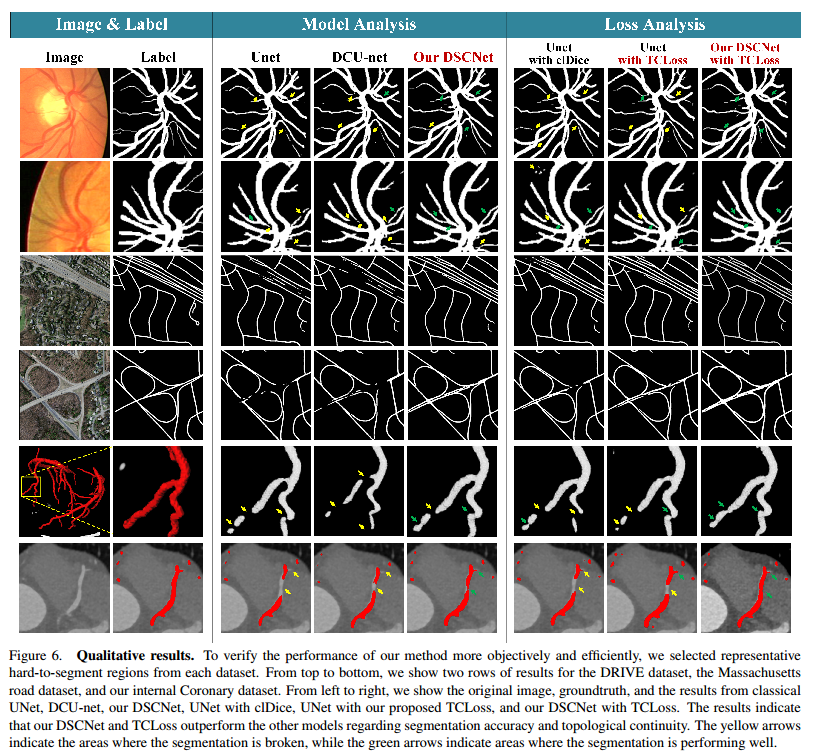
我们的DSCNet和TCLoss在任意方面都具有决定性的视觉优势(图6)。从左到右，第三到第五列显示了不同网络在分割精度方面的性能。由于我们的DSConv自适应地感知薄管结构的关键特征，我们的模型比其他方法更准确地关注特殊的管状特征，从而在管状结构分割方面表现出更好的性能。(2)证明tclos的有效性。从左至右，第6至第8列为不同损失函数对细管结构分割连续性的影响。加入我们提出的TCLoss后，在难以分割的区域中，分割的连续性大大提高。结果表明，该方法具有稳定的分割性能，具有较好的拓扑连续性，特别是在复杂多变的形态结构中。值得注意的是，在马萨诸塞州道路数据集上，我们的模型在相邻的直线或弯曲道路上实现了很好的可视化。更多的可视化结果可以在补充材料中找到。

5.3 模型分析

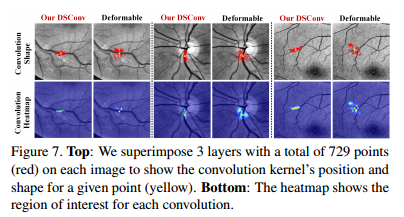
我们的DSConv可以动态地适应管状结构的形状，并且注意力与目标很好地吻合。(1)适应管状结构的形状。图7的顶部显示了卷积核的位置和形状。可视化结果表明，DSConv能很好地适应管状结构并保持形状，而可变形卷积在目标外徘徊。(2)关注管状结构的位置。图7的底部显示了给定点上的注意力热图。结果表明，DSConv最亮的区域集中在管状结构中，说明DSConv对管状结构更敏感。

5.4 未来工作

我们提出的框架能够很好地应对细管结构的分割，并成功地将形态学特征与拓扑知识相结合，指导模型适应分割。然而，其他形态学目标是否会在类似的范式下获得更好的性能仍然是一个令人兴奋的话题。同时更多的研究将对调查融合其他领域知识的可能性或进一步提高了拓扑分析的分割性能。进一步的实验和理论验证将使本课题更加丰富。

6. 结论

在本研究中，我们关注管状结构的特殊特征，并利用这些知识指导模型在特征提取、特征融合和损失约束三个阶段同时增强感知。首先，我们提出了一种动态蛇形卷积，自适应聚焦于细长和扭曲的结构，从而准确捕捉管状结构的特征。其次，引入多视角特征融合策略，弥补了特征融合过程中多角度关注特征的不足，保证了不同全局形态的重要信息被保留;最后，我们提出了拓扑连续性约束损失来约束分割的拓扑连续性。在二维和三维数据集上对该方法进行了验证，结果表明，与几种方法相比，该方法在管状结构分割任务上具有更好的准确性和连续性。