Guided Image Filtering

摘要

在本文中，我们提出了一种新型的显式图像滤波器——引导滤波器。 引导滤波器源自局部线性模型，通过考虑引导图像的内容生成滤波输出，引导图像可以是输入图像本身或另一幅不同的图像。引导滤波器可以像流行的双边滤波器 [1] 一样充当边缘保持平滑运算符，但在边缘附近具有更好的性能。 它还与抠图拉普拉斯矩阵[2]有理论联系，因此是比平滑算子更通用的概念，可以更好地利用引导图像中的结构。 此外，引导滤波器具有快速且非近似的线性时间算法，其计算复杂度与滤波核大小无关。 我们证明引导滤波 器在各种计算机视觉和计算机图形应用程序中既有效又高效，包括降噪、细节平滑/增强、HDR 压缩、图像抠图/羽化、去雾和联合上采样。

1.介绍

计算机视觉和计算机图形学中的大多数应用都涉及图像过滤的概念，以减少噪声和/或提取有用的图像结构。 高斯滤波器、拉普拉斯滤波器和 Sobel 滤波器等简单显式线性平移不变 (LTI) 滤波器广泛用于图像模糊/锐化、边缘检测和特征提取 [3]。 LTI 滤波还包括求解泊松方程的过程，例如在高动态范围 (HDR) 压缩 [4]、图像拼接 [5] 和图像抠图 [6] 中，其中滤波核隐式定义为 齐次拉普拉斯矩阵。

LTI 滤波器的内核是空间不变的，并且独立于任何图像内容。 但在许多情况下，我们可能希望在过滤过程中合并来自给定引导图像的附加信息。 例如，在着色 [7] 中，输出色度通道应与给定的亮度通道具有一致的边缘； 在图像抠图 [2] 中，输出 alpha 遮罩应该捕捉图像中的细微结构，如头发。 实现此目的的一种方法是优化二次函数，该函数通过考虑引导图像直接对未知输出施加一些约束。
然后通过求解用引导图像的信息编码的大稀疏矩阵来获得该解。 这个非齐次矩阵隐含地定义了一个translation-varient过滤内核。该方法应用在许多任务中，如着色[7]、图像消光[2]、多尺度分解[8]，以及去雾[9]。虽然这种基于优化的方法往往能产生带来最先进的质量，但它的代价是漫长的计算时间。

另一种方法是利用引导图像明确地建立滤波器核。双边滤波器，在[10]中提出，在[1]中流行，在[11]中被推广，也许是最流行的一种过滤器。它在一个像素的输出是附近像素的加权平均，其中的权重取决于强度/颜色的相似性。引导图像可以是
滤波器输入本身[1]或其他图像[11]。双边滤波器可以平滑小的波动并保留边缘。虽然这个滤波器在许多情况下是有效的、它在边缘附近可能会出现不需要的梯度反转伪影[12,13,8]（在第3.4节进一步解释）。它的快速实现也是一个具有挑战性的问题。最近的技术[14,15,16,17]依靠量化方法来加速，但是可能会牺牲精度。

2. 相关工作

2.1 双边滤波

双边滤波器将像素处的滤波器输出计算为相邻像素的加权平均值。 它在保留边缘的同时平滑图像。 由于这种良好的特性，它已被广泛用于降噪 [18]、HDR 压缩 [12]、多尺度细节分解 [19] 和图像抽象 [20]。 它被推广到 [11] 中的联合双边滤波器，其中权重是从另一个引导图像而不是滤波器输入计算的。 当滤波器输入不能可靠地提供边缘信息时，例如，当它非常嘈杂或者是中间结果时，联合双边滤波器特别受欢迎。 联合双边滤波器适用于flash/no-flash 去噪[11]、图像上采样[21]和图像反卷积[22]。

然而，已经注意到 [12,13,8] 双边滤波器在细节分解和 HDR 压缩中可能具有梯度反转伪影。 原因是当一个像素（通常在边缘）周围几乎没有相似像素时，高斯加权平均是不稳定的。 关于双边滤波器的另一个问题是它的效率。 蛮力实现在 O(Nr2) 时间内，当内核半径 r 很大时，这个时间过高，一个相似的解决办法是在离散空间颜色网格中获得。 最近，基于直方图开发了 O(N) 时间算法 [15,16]。 亚当斯等。 [17] 提出了一种彩色图像的快速算法。 以上所有方法都需要较高的量化程度才能达到令人满意的速度，但是是以质量下降为代价的。

2.2 基于优化的图像滤波

一系列的方法优化一个二次成本函数，求解一个线性系统，相当于用一个逆矩阵隐式过滤图像。在图像分割 [23] 和着色 [7] 中，该矩阵的亲和力是颜色相似度的高斯函数。 在图像抠图中，抠图拉普拉斯矩阵 [2] 旨在将 alpha 遮罩强制为图像颜色的局部线性变换。 该矩阵也适用于去雾[9]。 [8] 中的加权最小二乘 (WLS) 滤波器根据图像梯度调整矩阵亲和力，并对输入图像进行无晕分解。 虽然这些基于优化的方法通常会产生高质量的结果，但求解相应的线性系统非常耗时。
已经发现基于优化的过滤器与显式过滤器密切相关。 在 [24] 中，Elad 表明双边滤波器是求解高斯亲和矩阵的一次雅可比迭代。 在 [25] 中，Fattal 定义了edge-avoiding wavelets来近似 WLS 滤波器。 这些显式过滤器通常比基于优化的过滤器更简单、更快

3.引导滤波

我们首先定义一个通用的线性平移变量滤波过程，它涉及一个引导图像 I、一个输入图像 p 和一个输出图像 q。I和p都是根据应用预先给定的，它们可以相同。像素 i 处的滤波输出表示为加权平均值:

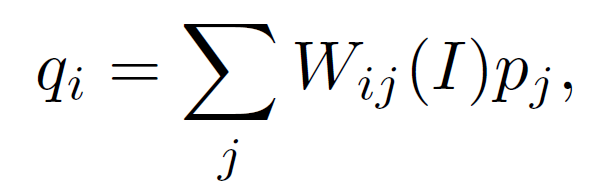
其中 i 和 j 是像素索引。 滤波器内核 Wij 是引导图像 I 的函数，与 p 无关。 该滤波器关于 p 是线性的。

这种滤波器的一个具体例子是联合双边滤波器 [11]。 双边滤波核 Wbf 由下式给出:

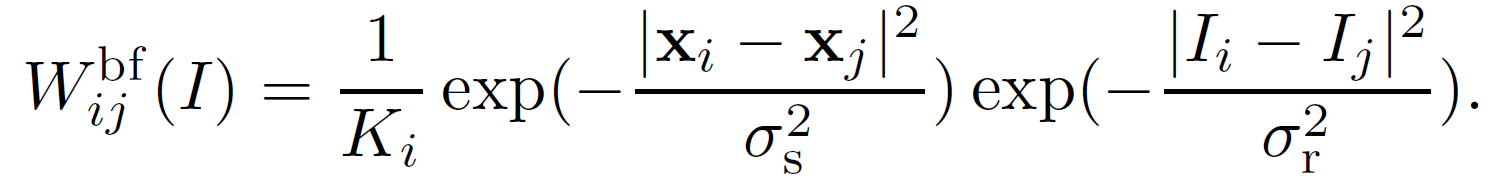
其中x为像素坐标，Ki为归一化参数确保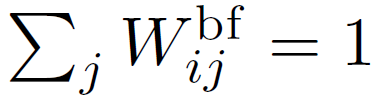
。参数σs和σr分别调节空间相似度和范围（强度/颜色）相似度。 当 I 和 p 相同时，联合双边滤波器退化为原始双边滤波器 [1].

3.1 定义

现在我们定义引导过滤器及其内核。 引导滤波器的关键假设是引导 I 和滤波器输出 q 之间的局部线性模型。 我们假设 q 是 I 在以像素 k 为中心的窗口 ωk 中的线性变换：

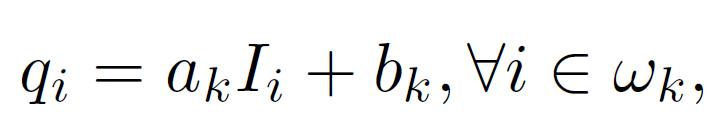
其中 (ak, bk) 是假设在 ωk 中恒定的一些线性系数。 我们使用一个半径为 r 的方形窗口。 这个局部线性模型确保只有当 I 有边时 q 才有边，因为 ∇q = a∇I。 该模型已被证明在图像抠图 [2]、图像超分辨率 [26] 和去雾方面很有用。

为了确定线性系数，我们寻求 (3) 的一个解决方案，使 q 和滤波器输入 p 之间的差异最小化。 具体来说，我们最小化窗口中的以下成本函数：

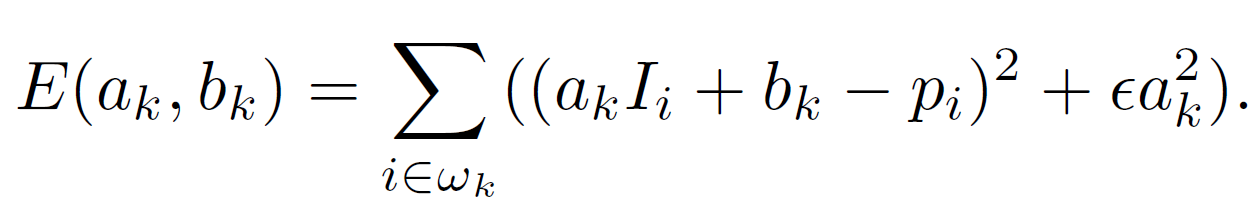
这里ε是防止 ak 太大的正则化参数。 我们将在 3.2 节中研究它的重要性。 (4) 的解可以通过线性回归给出：

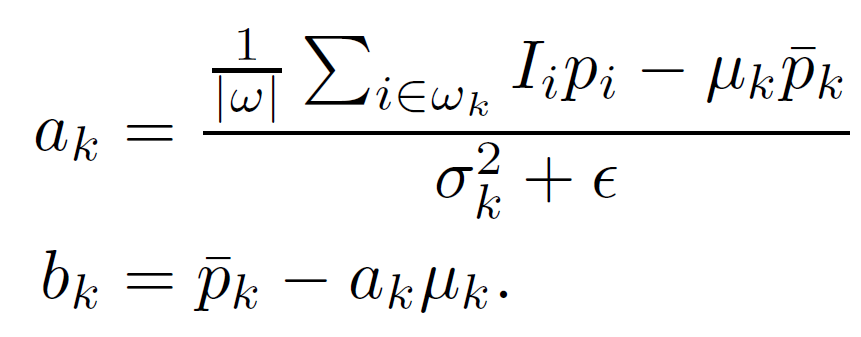
这里，μk 和 σk² 是 I 在 ωk 中的均值和方差，|ω| 是 ωk 中的像素数，

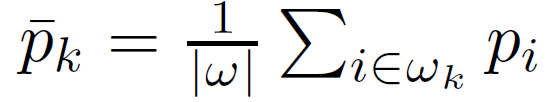
是 p 在 ωk 中的平均值。

接下来我们将线性模型应用于整个图像中的所有局部窗口。但是，一个像素i涉及到所有包含i的窗口ωk，所以式(3)中的qi在不同窗口计算时的值是不一样的。 一个简单的策略是对所有可能的 qi 值进行平均。 因此，在为图像中的所有补丁 ωk 计算 (ak, bk) 之后，我们通过以下方式计算滤波器输出：

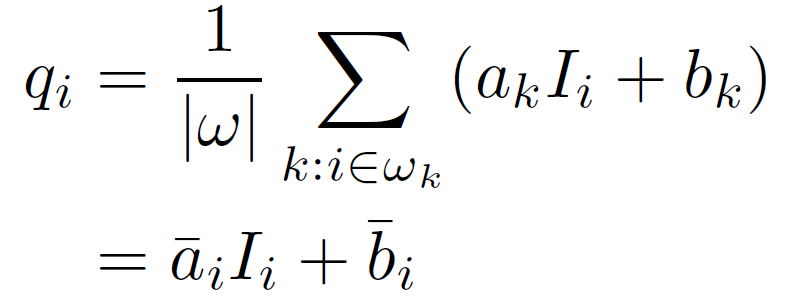
其中:

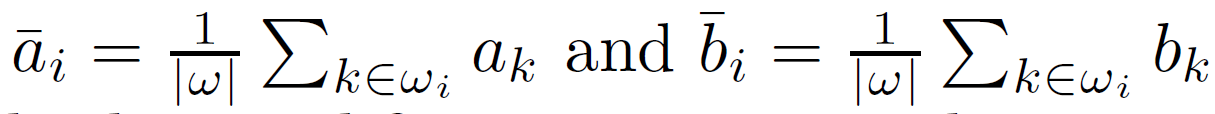
通过此修改，∇q 不再是 ∇I 的缩放，因为线性系数

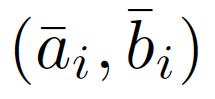
在空间上发生变化。 但由于
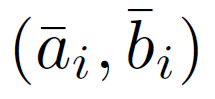是平均滤波器的输出，它们的梯度应该比强边缘附近的 I 的梯度小得多。在这种情况下，我们仍然可以有

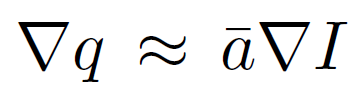
，这意味着 I 中的突然强度变化可以大部分保持在 q 中.

我们指出，式（5）、（6）、（8）给出的I、p、q之间的关系确实是图像滤波（1）的形式。 实际上，ak可以被写作p的加权和，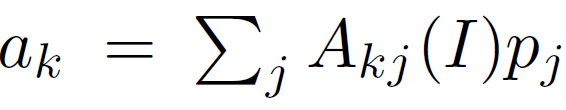
其中Aij是只依赖于I的权重，由于相同原因，我们有来自(6)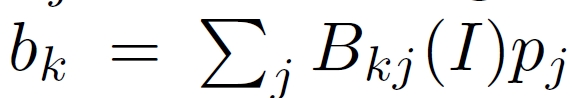和来自(8)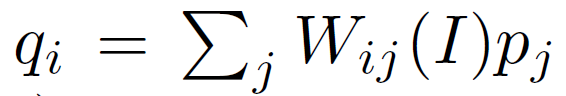，可以证明（见补充材料）内核权重可以明确表示为：

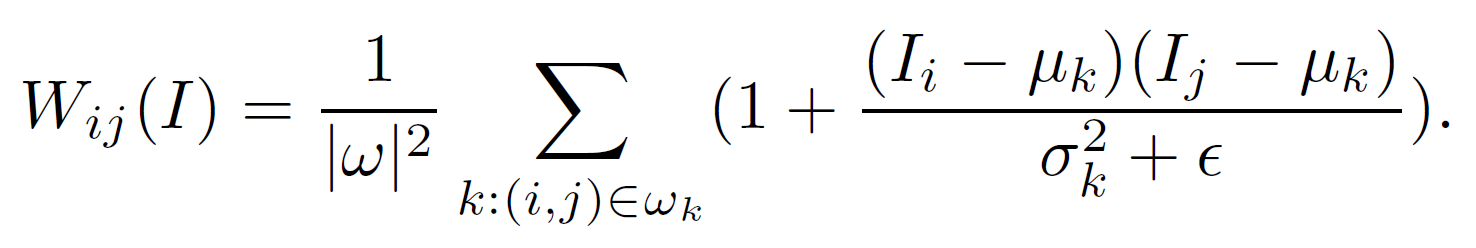
一些进一步的计算表明 j Wij (I) = 1。不需要额外的努力来标准化权重。

3.2 边缘保持滤波

图 1（顶部）显示了具有各种参数集的引导滤波器的示例。
我们可以看到它具有保边平滑特性。 这可以直观地解释如下。 考虑 I = p 的情况。 很明显，如果ε = 0，则 (4) 的解是 ak = 1 和 bk = 0。如果ε > 0，我们可以考虑两种情况:
Case1:“Flat Patch”。 如果图像 I 在 ωk 中是常数，则 (4) 由 ak = 0 和
$$b_k=\bar p_k$$
求解；
Case2: “高方差”。 如果图像 I 在 ωk 内变化很大，则 ak 趋近于 1，而 bk 趋近于 0
当 ak 和 bk 被平均得到
$$\bar a_k \bar b_k$$
，结合在（8）中得到输出，我们有如果一个像素在“高方差”区域的中间，那么它的值是不变的，而如果 它位于“平坦补丁”区域的中间，其值成为附近像素的平均值。
更具体地说，“平坦补丁”或“高方差”的标准由参数给出。 方差 (σ2) 远小于的补丁被平滑，而方差远大于的补丁被保留。 在引导滤波器中的效果类似于双边滤波器（2）中的范围方差σr²。 这两个参数都决定了“什么是边缘/应该保留的高方差补丁”。 图 1（底部）显示了双边滤波器结果作为比较。

3.3 过滤核

也可以通过研究滤波器核 (9) 来理解边缘保持平滑特性。 以一维信号的理想阶跃边沿为例（图 2）。当 Ii 和 Ij 位于边缘的同一侧时，Ii-μk 和 Ij-μk 项具有相同的符号 (+/-)，而当两个像素位于不同侧时，它们具有相反的符号。所以在(9)

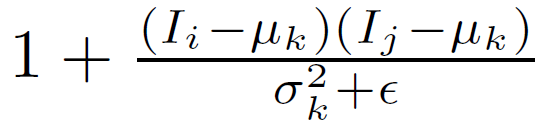
对于不同侧的两个像素比相同侧的两个像素小得多（并且接近于零）。 这意味着边缘上的像素几乎不会一起平均。 我们也可以理解from(9)中ε的平滑效果。当
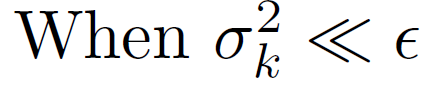卷积核变成
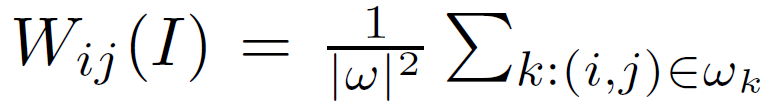这是一个低通滤波器，不会偏置边缘的任何一侧。

图 3 显示了真实图像中内核形状的两个示例。 顶行是靠近阶梯边缘的内核。 与双边内核一样，引导滤波器的内核将几乎为零的权重分配给边缘另一侧的像素。底行是具有小比例纹理的补丁中的内核。 这两个滤波器将几乎所有附近的像素平均在一起，并显示为低通滤波器。

3.4 梯度保持滤波

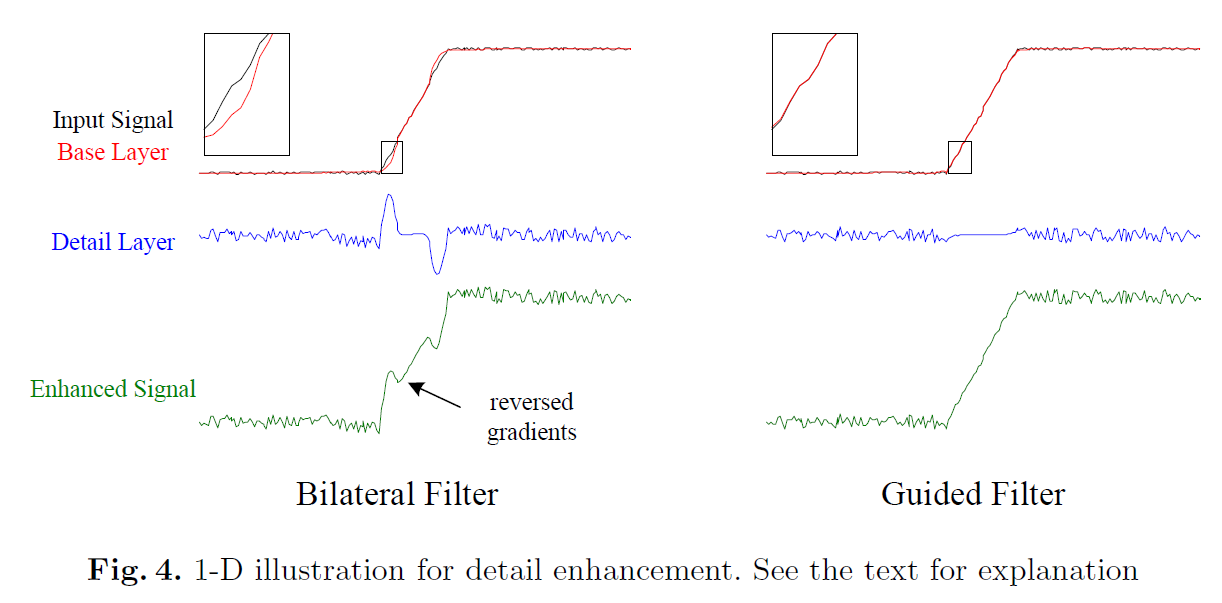
虽然引导滤波器与双边滤波器一样是一种边缘保持平滑滤波器，但它避免了细节增强和 HDR 压缩中可能出现的梯度反转伪影。 图 4 显示了细节增强的一维示例。
给定输入信号（黑色），它的边缘保持平滑输出用作基础层（红色）。 输入信号和基础层之间的区别是细节层（蓝色）。 它被放大以增强细节。 增强信号（绿色）是增强细节层和基础层的组合。 在 [12] 中可以找到对该方法的详细描述。

对于双边滤波器（图 4 左），基础层与边缘像素处的输入信号不一致。 这是因为它们周围很少有像素具有相似的颜色，高斯加权平均的统计数据很少，变得不可靠。 所以细节层有很大的波动，重组后的信号出现如图所示的反向梯度。 另一方面，引导滤波器（图 4 右）更好地保留了 I 中的梯度信息，因为基础层的梯度在边缘附近为 ∇q ≈ ¯a∇I。 边缘的形状在重组层中得到很好的保持

3.5 与Matting Laplacian 矩阵的关系

引导滤波器不仅可以用作平滑算子。 它也与抠图拉普拉斯矩阵密切相关[2]。 这为引导过滤器带来了新的见解，并激发了一些新的应用。

在抠图 [2] 的封闭形式解中，抠图拉普拉斯矩阵源自局部线性模型。 与为每个窗口计算局部最优的引导滤波器不同，封闭形式的解决方案寻求全局最优。为了求解未知的 alpha 遮罩，此方法最小化以下成本函数：

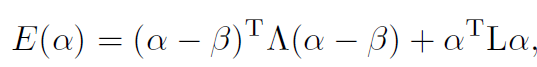
其中 α 是以矩阵形式表示的未知 alpha matte，β 是约束（例如，trimap），L 是 N×N matting Laplacian 矩阵，Λ 是用约束权重编码的对角矩阵。 此优化问题的解决方案通过求解线性系统给出：(L + Λ)α = Λβ。

抠图拉普拉斯矩阵的元素由下式给出：

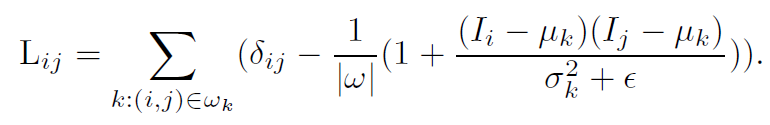
其中 δij 是克罗内克三角洲。 比较（11）和（9），我们发现抠图拉普拉斯矩阵的元素可以直接由引导滤波器核权重给出：

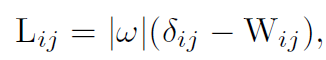
按照[24]中的策略，我们可以进一步证明（见补充材料）引导滤波器的输出是优化（10）中的一次雅可比迭代。如果 β 是对遮罩的合理猜测，我们可以运行一个 Jacobi 步骤并通过引导过滤过程获得 (10) 的近似解：αi ≈ j Wij (I)βj 。 在第 4 节中，我们将此属性应用于图像抠图/羽化和去雾。

3.6 O(N)时间提取算法

引导滤波器相对于双边滤波器的另一个优势是它自动具有 O(N) 时间精确算法。 O(N) 时间意味着时间复杂度与窗口半径 r 无关，因此我们可以在应用程序中自由使用任意大小的内核

(1) 中的过滤过程是平移变体卷积。 当内核变大时，其计算复杂度会增加。 我们不是直接执行卷积，而是根据其定义 (5)(6)(8) 计算滤波器输出。 这些等式中的所有求和都是盒式滤波器 ( i∈ωk fi )。 我们应用 O(N) 时间积分图像技术 [28] 来计算盒式滤波器的输出。 因此引导滤波器可以在 O(N) 时间内计算出来。

O(N) 时间算法可以很容易地扩展到 RGB 颜色引导图像。 当在任何单个通道中无法区分边缘或细节时，使用颜色指导图像进行过滤是必要的。 为了推广到彩色引导图像，我们将局部线性模型 (3) 重写为：

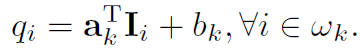
这里 Ii 是一个 3×1 颜色向量，ak 是一个 3×1 系数向量，qi 和 bk 是标量。 颜色引导图像的引导滤波器变为：

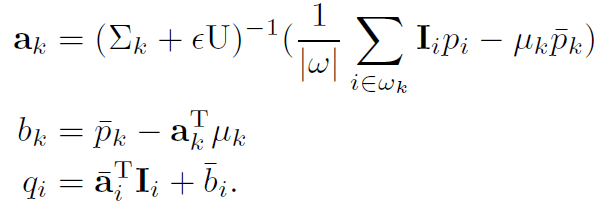
这里 Σk 是 I 在 ωk 中的 3×3 协方差矩阵，U 是 3×3 单位矩阵。
求和仍然是框过滤器，可以在 O(N) 时间内计算。

我们在配备 2.0Hz Intel Core 2 Duo CPU 的笔记本电脑上测试运行时间。 对于灰度引导滤波器，处理 1 兆像素图像需要 80 毫秒。 作为比较，[15] 中的 O(N) 时间双边滤波器使用 32 个 bin 的直方图需要 42ms，使用 64 个 bin 需要 85ms。 请注意，引导滤波器算法是非近似的，适用于高位深度的数据，而 O(N) 时间双边滤波器可能具有明显的量化伪像（见图 5）。 [16] 中的算法使用 8 个 bin（使用作者网站上的公共代码）每百万像素需要 1.2 秒。 对于 RGB 制导图像，制导滤波器处理一张 1 兆像素图像大约需要 0.3 秒。 [16]中的高维双边滤波器算法平均需要大约 10 秒来处理每 100 万像素的 RGB 图像。

4. 应用和实验结果

在本节中，我们将引导过滤器应用于各种计算机视觉和图形应用程序

细节增强和 HDR 压缩。 细节增强的方法在 3.4 节中描述。 对于 HDR 压缩，我们压缩基础层而不是放大细节层。 图 6 显示了细节增强的示例，图 7 显示了 HDR 压缩的示例。 还提供了使用双边滤波器的结果。 如放大图所示，双边滤波器导致梯度反转伪影。

闪光/无闪光降噪。 在 [11] 中，建议在其 flash 版本的指导下对非 flash 图像进行降噪。 图 8 显示了使用联合双边滤波器和引导滤波器的比较。 在联合双边滤波结果的某些边缘附近，梯度反转伪影很明显。

消光/引导羽化。 我们将引导过滤器用作引导羽化：细化二元掩码以在对象边界附近出现 alpha 遮罩。（图9）。 二值掩码可以从图切割或其他分割方法中获得，并用作滤波器输入 p。 引导 I 是彩色图像。 在商业软件 Adob​​e Photoshop CS4 中可以找到类似的功能“Refine Edge”。 我们还可以使用封闭形式的解决方案 [2] 来计算精确的遮罩。 在图 9 中，我们将我们的结果与 Photoshop Refine Edge 和封闭形式的解决方案进行了比较。 我们的结果在视觉上与这个短发案例中的封闭形式解决方案相当。 我们的方法和 Photoshop 都为这个 6 兆像素的图像提供快速反馈 (<1s)，而封闭形式的解决方案需要大约两分钟来解决一个巨大的线性系统。

单图像雾度去除。 在[9]中，使用暗通道先验粗略估计了雾度传输图，并通过求解抠图拉普拉斯矩阵对其进行了细化。 相反，我们简单地过滤下的原始传输图在模糊图像的指导下。结果在视觉上是相似的（图 10）。 引导过滤器处理这个 600×400 彩色图像大约需要 0.1 秒，但运行时间超过 10 秒，如 [9] 中所述

联合上采样。 联合上采样[21]是在另一幅图像的引导下对一幅图像进行上采样。 以着色[7]的应用为例。通过优化过程对灰度亮度图像进行着色。为了减少运行时间，色度通道在粗分辨率下求解，并在全分辨率亮度图像的引导下通过联合双边滤波器 [21] 进行上采样。 这个上采样过程也可以由引导滤波器执行。 结果在视觉上具有可比性（图 11）。

5 讨论与结论

在本文中，我们提出了一种广泛应用于计算机视觉和图形学的新型滤波器。 与最近加速双边滤波器 [14,15,16,17] 的趋势不同，我们定义了一种新型滤波器，它具有边缘保持平滑的良好特性，但可以高效准确地计算。 我们的过滤器更通用，可以处理超出“平滑”概念的一些应用。 由于局部线性模型（3）可以被视为一个简单的学习案例，因此可以应用其他高级模型/特征来获得新的过滤器。

作为基于本地的运算符，引导过滤器不能直接适用于像笔画这样的稀疏输入。 它还具有其他显式过滤器的共同限制 - 它可能在某些边缘附近有光晕。 事实上，对于低级和本地操作员来说，确定应该平滑哪些边缘以及应该保留哪些边缘是不明确的。 不适当地平滑边缘会导致其附近出现光晕。然而，我们相信引导滤波器的简单性和高效性在许多情况下仍然是有益的