引言
今天继续花书中基础部分,第四章关于数值计算的介绍,虽然听起来有点无聊,但还是一起来看看吧!
正文
上溢和下溢
上溢就是本来很小的数扩大了,比如很大数量级的数被近似为无穷
下溢在实际情况中更容易发生就是四舍五入把数值缩小了,主要因为计算机的表示精度都是有限的,每种数据类型都有自己的表示精度,举个例子,在python中输入1/3*3结果并不为1
一个解决办法就是用softmax函数
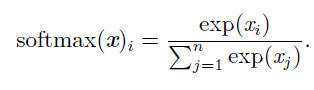
病态条件
只要指输出对输入十分敏感,输入轻微变化,输出变化很大,在不同应用场景各有利弊
基于梯度的优化方法
对于单变量,优化指的是改变x 以最小化或最大化某个函数f(x) 的任务,把要最小化或最大化的函数称为目标函数,当我们对其进行最小化时,我们也把它称为代价函数(损失函数),我们通常使用一个上标表示最小化或最大化函数的x值。如我们记$x^=argminf(x)$。
说到这里肯定离不开梯度下降法,其实梯度下降法的核心就是函数的链式求导则,导数它表明如何缩放输入的小变化才能在输出获得相应的变化,当导数为0时导数不能表明函数值往哪个方向变化,这里我们要区分以下几个点:
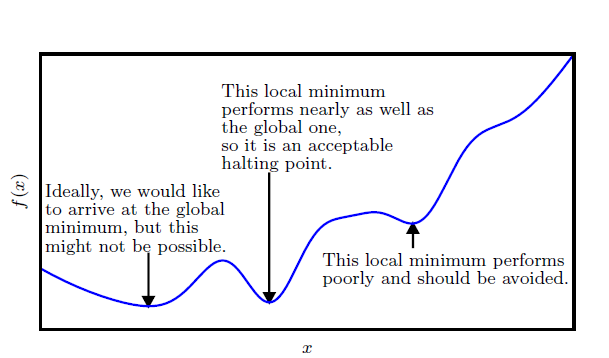
- 极值点:某点的函数值f(x)大于或者小于周围点,可以理解成小山谷和小山顶
- 鞍点:临界点值不是最大也不是最小,可以理解成地理学中的鞍点
- 最小值点:整体最大值或者最小值点,通常是我们的优化目标,可以理解成珠穆朗玛峰(世界最高峰)
对于多变量,我们需要用到偏导数,偏导数$\frac{\partial}{\partial x_i}f(x)$衡量点x 处只有xi 增加时f(x) 如何变化,梯度(gradient)是相对一个向量求导的导数:f的导数是包含所有偏导数的向量,记为$\bigtriangledown_xf(x)$,梯度的第i 个元素是f 关于xi 的偏导数,多变量情况下临界点是梯度中所有元素均为0.
在u(单位向量)方向的方向导数是函数f 在u 方向的斜率,方向导数是函数f(x+αu)关于α的导数,使用链式求导法则,当α=0时,
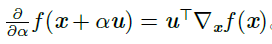
为了最小化f,我们希望找到使f 下降得最快的方向,计算方向导数:
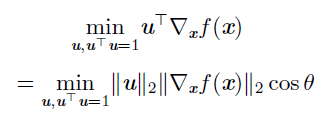
其中θ是u 与梯度的夹角。将$|u|=1$ 代入,并忽略与u 无关的项,可以简化得到$\mathop\limits_u cos\theta$,这在u 与梯度方向相反时取得最小,们在负梯度方向上移动可以减小f。这被称为梯度下降法:
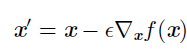
其中ε为学习率,学习率要适中,太大可能会使得函数跳过极值点,太小训练次数太多,计算成本太高,梯度下降法有很多问题,后面有很多针对性改进方案,比如随机梯度下降(SGD),Momentem(动量),后面会出专门章节来说明。
Jacobin矩阵和Hessian矩阵
这两个矩阵是很多优化算法的基础,但是我觉得书上讲的并不好,下面是个人理解:
- Jacobin矩阵:
是一阶偏导数以一定方式排列成的矩阵,通俗理解就是输出y用n个表示,每个输出yi对m个输入变量中的每个变量进行求导,排列而成的矩阵就是雅可比矩阵。
对于函数$f: \mathbbm\rightarrow \mathbbn$,f的Jacobin矩阵定义为:$J_=\frac{\partial}{\partial x_j} f(x)_i$,如下图所示

如果p是Rn中一点,在这点导数用JF(p)表示,由F(p)描述的线性算子就是接近点P的F的最优线性逼近,表示为:
$F(x) \approx F(p)+J_F(p)\times(x-p)$
当m=n,矩阵为方阵,可以求取行列式,称为Jacobin行列式 - Hessian矩阵
是一个自变量为向量的实值函数的二阶偏导数组成的方块矩阵,此函数表示为:
$f(x_1,x_2,...x_n)$,如果f的所有二阶导数都存在,f的海森矩阵可以表示为:
$H(f)(x)=D_iD_jf(x)$,其中$x=(x_1,x_2,...x_n)$,Hessian 等价于梯度的Jacobian 矩阵,H(f)表示为:
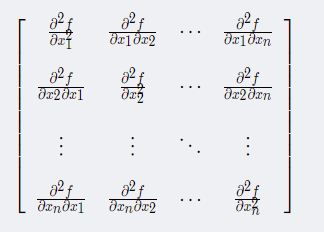
微分算子在任何二阶偏导连续的点处可交换,也就是它们的顺序可以互换:
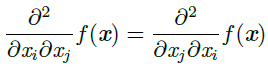
这意味着$H{i,j}=H_$,Hessian 矩阵在这些点上是对称的。因为Hessian 矩阵是实对称的,我们可以将其分解成一组实特征值和一组特征向量的正交基。在特定方向d上的二阶导数可以写成$d^THd$。当d是H 的一个特征向量时,这个方向的二阶导数就是对应的特征值。对于其他的方向d,方向二阶导数是所有特征值的加权平均,权重在0 和1 之间,且与d 夹角越小的特征向量的权重越大。最大特征值确定最大二阶导数,最小特征值确定最小二阶导数。
海森矩阵和凸优化问题很有关系,简单地说,海森矩阵正定- 函数的二阶偏导数恒大于0
- 函数的变化率(斜率)即一阶导数始终处于递增状态
- 函数为凸
因此,在诸如牛顿法等梯度方法中,使用海森矩阵的正定性可以非常便捷的判断函数是否有凸性,也就是是否可收敛到局部/全局的最优解。
- 正定性判别
这里补充一下正定性判别方法:- 若所有特征值均不小于零,则称为半正定
- 若所有特征值均大于零,则称为正定
- 多元函数Hessian矩阵半正定就相当于一元函数二阶导非负;多元函数为凸函数的充要条件为其二阶Hessian矩阵半正定
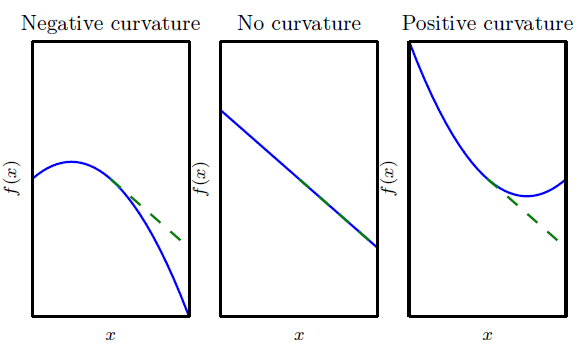
二阶导数是对曲率的衡量。假设我们有一个二次函数(虽然很多实践中的函数都不是二次的,但可以近似二次)这样的函数具有零二阶导数,那就没有曲率。也就是一条完全平坦的线,仅用梯度就可以预测它的值。我们使用沿负梯度方向大小为ϵ 的下降步,当该梯度是1 时,代价函数将下降ϵ。如果二阶导数是负的,函数曲线向下凹陷(向上凸出),因此代价函数将下降的比ϵ 多,如果二阶导数是正的,函数曲线是向上凹陷(向下凸出),因此代价函数将下降的比ϵ 少,如下图所示:
- 结合泰勒公式
我们在当前点x(0) 处作函数f(x) 的近似二阶泰勒级数:
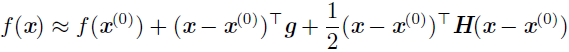
其中g 是梯度,H 是x(0) 点的Hessian矩阵。如果我们使用学习率ϵ,那么新的点x 将会是$x^{(0)}-\epsilon g$。代入上述的近似,可得:
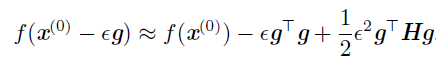
包含以下三项:- 函数原始值
- 函数斜率变化校正
- 函数曲率变化校正
最后一项太大,梯度下降可能向上移动,当$gTHg \le 0$时,ε将使f下降,当$gTHg \lt 0$时,泰勒级数下降最优步长为:
$\epsilon*=\frac{gTg}{g^THg}$,最坏的情况下,g 与H 最大特征值$\lambda_$ 对应的特征向量对齐,则最优步长是$\frac{1}{\lambda_}$,我们要最小化的函数能用二次函数很好地近似的情况下,Hessian矩阵 的特征值决定了学习率的量级。
同时由微积分的知识可知阶导数还可以被用于确定一个临界点是否是局部极大点、局部极小点或鞍点,对$f(x)'=0$分成以下三种情况:
- f′′(x) > 0 极小值点
- f′′(x) < 0 极大值点
- f′′(x) = 0 不确定
在多维情况下,我们需要检测函数的所有二阶导数,利用Hessian 的特征值分
解,我们可以将二阶导数测试扩展到多维情况。在临界点处(∇xf(x) = 0),我们通过检测Hessian 的特征值来判断该临界点是一个局部极大点、局部极小点还是鞍点。 - Hessian正定 极大值点
- Hessian负定 极小值点
- Hessian矩阵特征值有正有负 x 是f 某个横截面的局部极大点,却是另一个横截面的局部极小点,如下图所示:
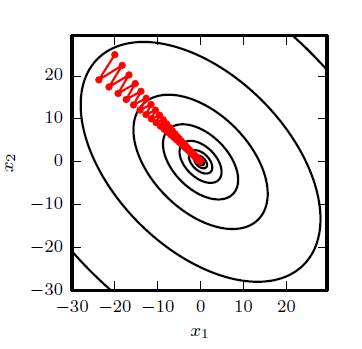
多维情况下,单个点处每个方向上的二阶导数是不同。Hessian 的条件数衡量 这些二阶导数的变化范围。当Hessian 的条件数很差时,梯度下降法也会表现得很差。这是因为一个方向上的导数增加得很快,而在另一个方向上增加得很慢。梯度下降不知道导数的这种变化,所以它不知道应该优先探索导数长期为负的方向。病态条件也导致很难选择合适的步长。步长必须足够小,以免冲过最小而向具有较强正曲率的方向上升。这通常意味着步长太小,以致于在其他较小曲率的方向上进展不明显。
这时候可以采用牛顿法,牛顿法基于一个二阶泰勒展开来近似x(0) 附近的f(x):
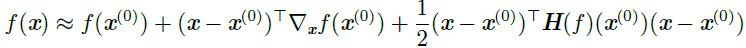
当f是正定二次函数时,牛顿法仅需要一步就可以跳到函数最小点,当f可以局部近似为正定二次,牛顿法需要多次迭代,迭代地更新近似函数和跳到近似函数的最小点可以比梯度下降更快地到达临界点。仅使用梯度信息的优化算法被称为一阶优化算法,使用Hessian 矩阵的优化算法被称为二阶最优化算法。
- Lipschitz函数
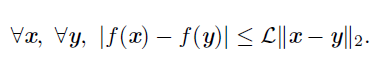 ,这个属性允许我们量化我们的假设——梯度下降等算法导致的输入的微小变化将使输出只产生微小变化
,这个属性允许我们量化我们的假设——梯度下降等算法导致的输入的微小变化将使输出只产生微小变化
约束优化
约束优化的一个简单方法是将约束考虑在内后简单地对梯度下降进行修改。如果我们使用一个小的恒定步长ϵ,我们可以先取梯度下降的单步结果,然后将结果投影回S。如果我们使用线搜索,我们只能在步长为ϵ 范围内搜索可行的新x 点,或者我们可以将线上的每个点投影到约束区域。
KKT算子
为了定义Lagrangian,我们先要通过等式和不等式的形式描述S。我们希望通
过m 个函数$g{(i)}$和n 个函数$h{(j)}$ 描述S,那么S 可以表示为$\mathbb={x|\forall i,g{(i)}(x)=0 and \forall j, h{(j)}(x)<0}$其中涉及g(i) 的等式称为等式约束,涉及h(j) 的不等式称为不等式约束,我们为每个约束引入新的变量λi 和αj,这些新变量被称为KKT 乘子,定义为:
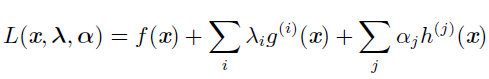
现在,我们可以通过优化无约束的广义Lagrangian 解决约束最小化问题。只要
存在至少一个可行点且f(x) 不允许取$\infty$,那么:
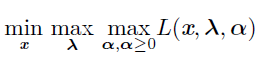
与如下函数有相同的最优目标函数值和最优点集x
$\mathop\limits_{x \in \mathbb}f(x)$
当约束满足时:
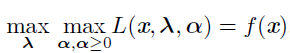
不满足时:
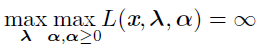
要解决约束最大化问题,我们可以构造f(x) 的广义Lagrange 函数,从而导
致以下优化问题:
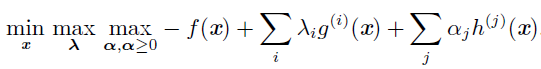
转化为:
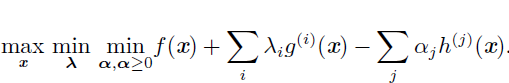
等式约束对应的λi的符号不重要,可以任意定义成加法或者减法,不等式约束分为以下两种情况:
- $h{(i)}(x*)=0$:约束为活跃的
- 其他,约束不活跃,有该约束的解和去掉该约束的解存在一组相同局部解,书上下面的解释到现在我也没看懂(后面再补充)
KKT条件
使用一组简单的性质来描述约束优化问题的最优点,称为KKT条件:
- 广义Lagrangian 的梯度为零。
- 所有关于x 和KKT 乘子的约束都满足
- 不等式约束显示的“互补松弛性”:α⊙ h(x) = 0
