引言

今天带来的是花书中关于机器学习的基础知识，一起来看看吧

正文

机器学习任务

分类
输入缺失分类（标注数据不完善）
回归
转录：观测一些相对非结构化表示的数据，并转录信息为离散的文本形式
机器翻译
结构化输出：输出的元素之间具有相关关系
异常检测
其他几个任务我个人觉得挺扯的

容量、欠拟合和过拟合

容量就是样本大小，欠拟合和过拟合的概念之前就提过了

超参数和验证集

超参数：不用学习，预先设定
验证集：调整参数

估计、偏差和方差

估计（不懂翻翻概率论）
- 点估计：为一些感兴趣的量提供单个‘‘最优’’ 预测。一般地，感兴趣的量可以是单个参数，或是某些参数模型中的一个向量参数
- 函数估计：估计函数关系
偏差
方差

最大似然估计

基本概念

考虑一组含有m 个样本的数据集$X={x^{(1)},...x{(m)}}$，独立地由未知的真实数据生成分布$p_(x)$生成，对θ最大似然估计：

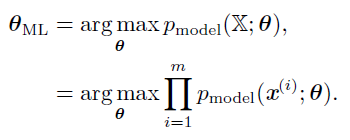
用对数表示：

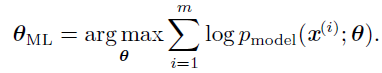
因为当我们重新缩放代价函数时arg max 不会改变，我们可以除以m 得到和训练数据经验分布^pdata 相关的期望作为准则：

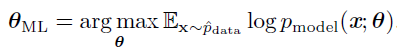
KL散度

一种解释最大似然估计的观点是将它看作最小化训练集上的经验分布$\hat$和模型分布之间的差异，两者之间的差异程度可以通过KL 散度度量。KL 散度被定义为:

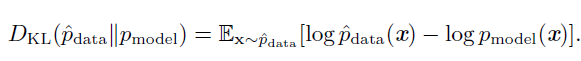
左边一项仅涉及到数据生成过程，和模型无关。这意味着当我们训练模型最小化KL
散度时，我们只需要最小化：

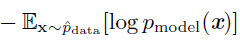
最小化KL 散度其实就是在最小化分布之间的交叉熵，我们可以将最大似然看作是使模型分布尽可能地和经验分布^pdata 相匹配的尝试。

交叉熵

书上还提到对于交叉熵很直白的理解：
任何一个由负对数似然组成的损失都是定义在训练集上的经验分布和定义在模型上的概率分布之间的交叉熵。例如，均方误差是经验分布和高斯模型之间的交叉熵

我们可以将最大似然看作是使模型分布尽可能地和经验分布^pdata 相匹配的尝试。理想情况下，我们希望匹配真实的数据生成分布pdata

条件对数似然

最大似然估计很容易扩展到估计条件概率$P(y|x;\theta)$，从而给定x 预测y,如果X 表示所有的输入，Y 表示我们观测到的目标，那么条件最大似然估计是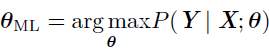
如果假设样本是独立同分布的，那么这可以分解成:

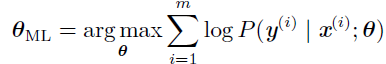
MSE

由于假设样本是独立同分布的，条件对数似然如下：

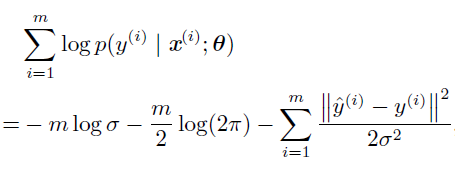
其中^y(i) 是线性回归在第i 个输入x(i) 上的输出，m 是训练样本的数目。对比均方误差和对数似然：

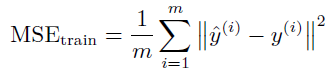
最大似然性质

在合适的条件下，最大似然估计具有一致性（参考第5.4.5 节），意味着训练样
本数目趋向于无穷大时，参数的最大似然估计会收敛到参数的真实值，这些条件是：

真实分布pdata 必须在模型族pmodel 中。否则，没有估计可以还原pdata。
真实分布pdata 必须刚好对应一个θ值。否则，最大似然估计恢复出真实分布pdata 后，也不能决定数据生成过程使用哪个θ

SGD

机器学习算法中的代价函数通常可以分解成每个样本的代价函数的总和。例如，训练数据的负条件对数似然可以写成：

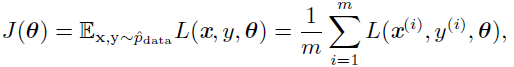
其中L 是每个样本的损失L(x,y,θ) = -log p(y | x; θ),对于这些相加的代价函数，梯度下降需要计算:

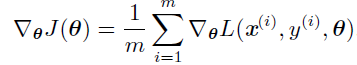
这个运算的计算代价是O(m)。随着训练集规模增长为数十亿的样本，计算一步梯度也会消耗相当长的时间。随机梯度下降的核心是，梯度是期望。期望可使用小规模的样本近似估计。具体而言，在算法的每一步，我们从训练集中均匀抽出一小批量（minibatch）样本{x1,...xm'}，小批量的数目m′ 通常是一个相对较小的数，并且通常是固定的，梯度估计可以表示成：

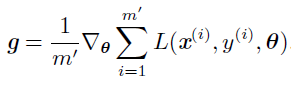
使用来自小批量B的样本，随机梯度下降算法使用如下的梯度下降估计：

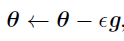
其中ε是学习率