引言

我们都知道线性模型是机器学习分类和回归的基础，那么今天就来重温一下基础吧！

正文

1. 线性模型

给定由d 个属性描述的示例$x=(x_1,x_2,...x_d)$ ，其中xi是x在第i个属
性上的取值，线性模型(linear model)试图学得一个通过属性的线性组合来进行
预测的函数，即：

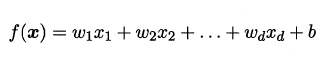
一般用向量形式写成：

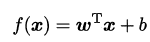
非线性模型可以通过线性模型堆叠生成

2. 线性回归

给定数据集$D={(x_1,y_1),...(x_m,y_m)}$，$x_i=(x_,x_,...x_)$,"线性回归"试图学得一个线性模型以尽可能准确地预测实值输出标记.

根据输入属性可以分成以下几种情况：

属性值间存在"序" (order)关系
可通过连续化将其转化为连续值，比如身高属性高和矮取值{1,0}，高、中、矮可以取值{1,0.5,0}，
属性值间不存在序关系
假定有k 个属性值，则通常转化为k 维向量，用One-hot编码，

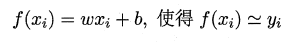
线性回归闭式解
通常采用均方误差来衡量f(x)和y，为了使得均方误差最小化：

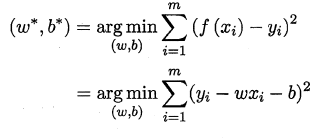
基于均方误差最小化来进行模型求解的方法称为"最小二乘法"，在线性回归中，最小二乘法就是试图找到一条直线，使所有样本到直线上的欧氏距离之和最小.求解ω 和b 使$E_{(w,b)=\sum^{m_(y_i-wx_i-b)}2}$最小化的过程，称为线性回
模型的最小二乘"参数估计",$E_{(w,b)}$分别对w和b求导，令导数为0得到最优解的闭式解：
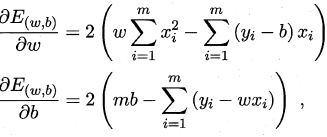
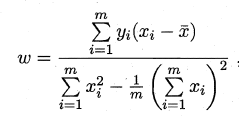
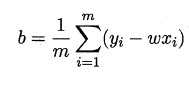
最小二乘法估计
我们把ω和b 吸收入向量形式$\hat w=(w,b)$ ，相应的把数据集D 表示为一个m x (d+1)大小的矩阵X ，其中每行对应于一个示例，该行前d 个元素对应于示例的d 个属性值，最后一个元素恒置为1 ，即
再把标记也写成向量形式$y=(y_1,y_2,...y_m)$ ，有:

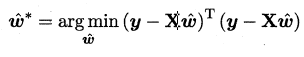
令

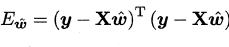
对$\hat w$求导，有：

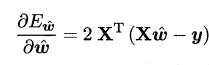
令上式为0即可得到闭式解，下面对$X^TX$进行讨论:
- 满秩:
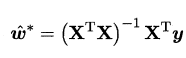
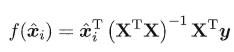
- 不满秩:
  引入正则化项

通常还采用对数回归使得输出标记在对应尺度上进行变化，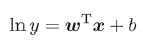
在试图让$e^{wTx+y}$逼近y ,得到广义线性回归模型：

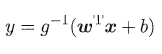
对数几率回归

很多时候我们需要把预测输出值$z=w^Tx+b$限定在(0,1)之间，可以让z通过sigmoid函数:

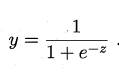
即

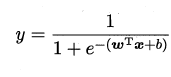
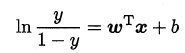
将y视为样本z 作为正例的可能性，则1-y 是其反例可能性，两者的比值$\frac{1-y}$称为几率，输出为正例的相对可能性，对数几率即为：

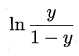
用线性回归模型的预测结果去逼近真实标记的对数几率，因此，其对应的模型称为"对数几率回归"，虽然它的名字是"回归"，但实际却是一种分类学习方法.

参数确定
y视为类后验概率估计$p(y=1|x)$，得到：

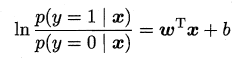
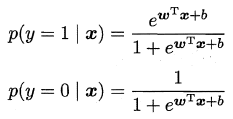
给定数据集${(x_i,y_i)}_^m$通过极大似然法：

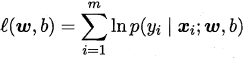
下面引用西瓜书上的推导过程：

最大化上式等价于最小化：

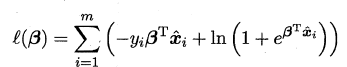
可用牛顿法或者梯度下降法求解：

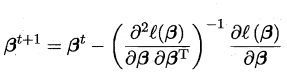
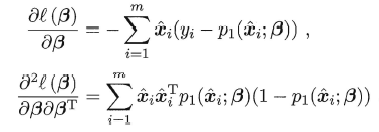
LDA(Fisher判别分析)

给定训练样例集，设法将样例投影到一条直线上，使得同类样例的投影点尽可能接近、异类样例的投影点尽可能远离;在对新样本进行分类时，将其投影到同样的这条直线上，再根据投影点的位置来确定新样本的类别.

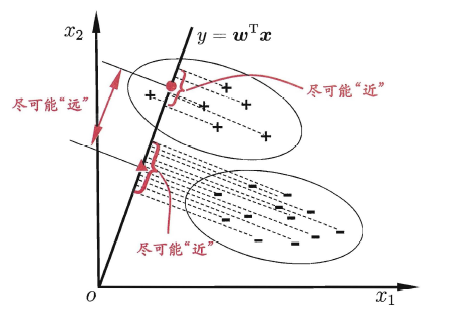
为了少打公式，下面应用原文（这一部分书上写的还是不错）

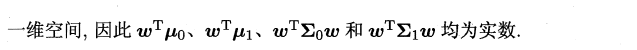
欲使同类样例的投影点尽可能接近，可以让同类样例投影点的协方差尽可能小，即$w^T\sum_0w+wT\sum_1w$尽可能小，欲使不同类直接距离尽可能大，可以让$|w^T\mu_0-wT\mu_1|^2_2$尽可能大，得到以下优化目标：

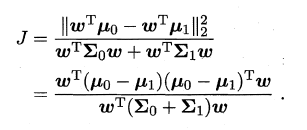
类内散度矩阵
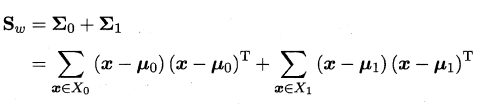
类间散度矩阵

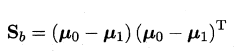
优化目标重写为:

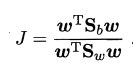
令$w^{TS_ww$= 1,上式等价为：

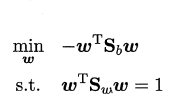
使用拉格朗日乘子法：

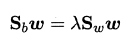
其中λ 是拉格朗日乘子.注意到$S_bw$的方向恒为$\mu_0-\mu_1$ ，不妨令:

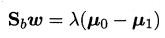
有:

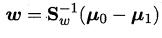
考虑到数值解的稳定性，在实践中通常是对Sw 进行奇异值分解，即$S_w=U\sum V}T$，这里$\sum$是一个实对角矩阵，其对角线上的元素是$S_w$的奇异值，然后再由$S_w^{-1}=V\sum{-1}U^T$得到$S_w{-1}$，同理也可以把LDA用在多分类任务中：
假定存在N 个类，且第i类示例数为叫mi，我们先定义"全局散度矩阵"

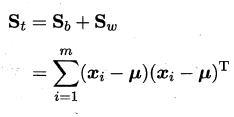
μ 是所有示例的均值向量.将类内散度矩阵$S_w$重定义为每个类别的散度矩阵之和，即:

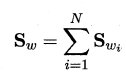
其中：

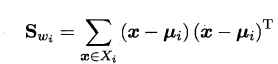
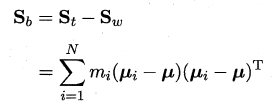
常见的一种实现是采用优化目标：

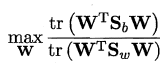
tr表示矩阵的迹，采用以下广义特征：

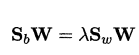
可以把N维降低到N-1维

多分类问题

可以采用以下几种策略：

一对一：拆成多个二分类
对N个类别，进行两两配对，从而产生N(N-1)/2 个二分类任务，例如区分i类和j类，可以把i类当成正类,j类当成反类
一对多：把i类当成正类，其余当成反类，有N个分类器
多对多: 把若干类别当成正类，其他当成反类，需要对正反类进行编码

ECOC：

编码：
对N个类别做M次划分，每次划分将一部分类别划为正类，一部分划为反类，从而形成一个二分类训练集;这样一共产生M个训练集，可训练出M 个分类器.
解码
M 个分类器分别对测试样本进行预测，这些预测标记组成一个编码.将这个预测编码与每个类别各自的编码进行比较，返回其中距离最小的类别作为最终预测结果.
类别划分
类别划分通过"编码矩阵"指定，常见有二元码和三元码，前者将每个类别分别指定为正类和反类，后者在正、反类之外，还可指定"停用类，西瓜书上的例子非常好，这里直接引用:

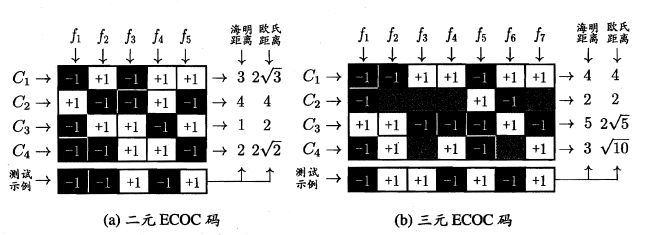
其中的欧式距离和海明距离可以参考我的另一篇博客:
http://121.40.183.153:8090/archives/%E6%9C%BA%E5%99%A8%E5%AD%A6%E4%B9%A0%E4%B8%AD%E5%B8%B8%E8%A7%81%E5%87%A0%E7%A7%8D%E8%B7%9D%E7%A6%BB
ECOC 编码对分类器的错误有一定的容忍和修正能力，一般分类器数量越多，纠错能力越强，但计算开销变大。

类别不平衡问题

样本中正负样本数目不均衡，这时输出阈值不能简单设定为0.5，可以设为：
$\frac{m^+}{m-}$，其中m+为正样本数目，m-为负样本数目